Проекция вектора на ось

Ориентированной осью называется прямая, на которой закреплена точка - начало отсчета, выбрана единица длины и направление отсчета.

Рис. 6

Проекцией вектора на ось называется величина, численно равная длине отрезка между основаниями перпендикуляров, опущенных из точек А и В на l. Эта длина берется со знаком плюс, если направление от 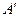к совпадает с направлением оси l и минус в противном случае (рис. 6). Аналогично определяется проекция одного вектора на другой.

Углом между осью и вектором называется угол, на который нужно повернуть ось до совмещения с вектором кратчайшим образом (так чтобы их стрелки совпали). Из такого определения следует, что .

Свойства проекции вектора на ось.

1.Проекция равна нулю тогда и только тогда, когда вектор перпендикулярен оси (говорят, вектор ортогонален оси).

2. При параллельном переносе вектора его проекция не меняется.

3. Проекция вектора на ось равна произведению длины вектора на

косинус угла между вектором и осью.

.

Рис. 7 Рис. 8

В этой формуле знак проекции регулируется знаком косинуса:

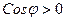- если острый угол (рис. 7), то и ;

- если тупой угол (рис. 8), то и .

4. Скалярный множитель можно выносить за знак проекции

.

5. Проекция суммы векторов равна сумме проекций слагаемых

.

Дата добавления: 2015-09-05