
Читайте также:
|
Базис называется ортонормированным, если его векторы попарно ортогональны и по длине равны единицам.
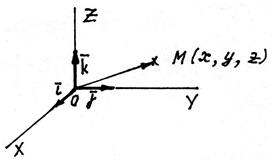 |
Рис. 9
 Базисные векторы такой системы называются ортами и обозначаются соответственно
Базисные векторы такой системы называются ортами и обозначаются соответственно 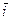 ,
,  ,
,  (рис. 9). Оси идущие в направлении базисных векторов соответственно OX – ось абсцисс, OY – ось ординат, OZ – ось аппликат. Система координат называется правой, если кратчайший поворот первого базисного вектора
(рис. 9). Оси идущие в направлении базисных векторов соответственно OX – ось абсцисс, OY – ось ординат, OZ – ось аппликат. Система координат называется правой, если кратчайший поворот первого базисного вектора 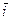 до совмещения со вторым базисным вектором
до совмещения со вторым базисным вектором  смотрится с конца третьего базисного вектора
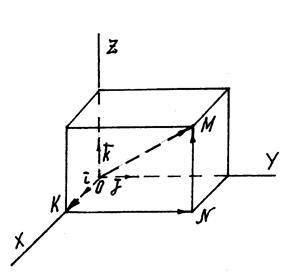
смотрится с конца третьего базисного вектора  происходящим против хода часовой стрелки. В противном случае имеем левую систему координат. Нетрудно видеть (рис. 10), что координатами вектора
происходящим против хода часовой стрелки. В противном случае имеем левую систему координат. Нетрудно видеть (рис. 10), что координатами вектора 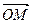 , равно как и точки М, являются проекции
, равно как и точки М, являются проекции 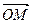 на координатные оси.
на координатные оси.
Рис. 10
Тогда 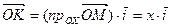 , аналогично
, аналогично 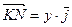 ,
,  . Теперь радиус-вектор
. Теперь радиус-вектор  или
или 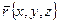 , где
, где  – координаты радиус-вектора
– координаты радиус-вектора  , а
, а  ,
, 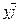 ,
,  - составляющие или компоненты этого вектора.
- составляющие или компоненты этого вектора. 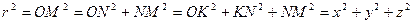 .
.
Поскольку, например,  , а
, а 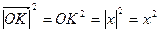 . Теперь
. Теперь 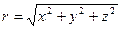 .
. 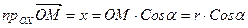 , где
, где 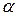 - угол между вектором
- угол между вектором  и осью OX. Теперь
и осью OX. Теперь  , аналогично
, аналогично 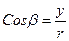 ,
, 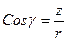 , где
, где 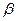 и
и 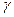 - углы между
- углы между  и осями OY и OZ соответственно. Приведенные косинусы называются направляющими косинусами радиуса вектора
и осями OY и OZ соответственно. Приведенные косинусы называются направляющими косинусами радиуса вектора  .
.
Если 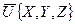 - произвольный вектор и X, Y, Z – его проекции на оси, то перенося начало
- произвольный вектор и X, Y, Z – его проекции на оси, то перенося начало 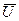 в точку О, будем иметь
в точку О, будем иметь 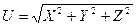 ,
,  ,
, 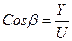 ,
, 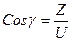 ,
, 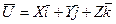 .
.
Если вектор задан координатами начала  и конца
и конца 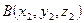 , то
, то 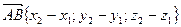 и расстояние
и расстояние  между точками А и В будет
между точками А и В будет 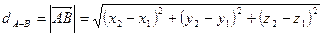 .
.
Дата добавления: 2015-09-05; просмотров: 94 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Проекция вектора на ось | | | Скалярное произведение двух векторов |