Читайте также:
|
Углом 
между двумя векторами называется угол, на который нужно повернуть один вектор до совмещения с другим кратчайшим образом. Из такого определения угла следует, что 
.
Скалярным произведением двух векторов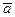 
и 
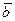называется число равное произведению длин векторов на косинус угла между ними:
.
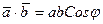В последней формуле точка – знак скалярного умножения векторов.
,
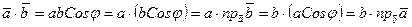таким образом, скалярное произведение равно произведению длины одного из векторов на проекцию второго вектора на первый.
Свойства скалярного произведения:
1. Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны: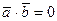 
.
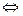
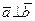2. Скалярный квадрат вектора равен квадрату скаляра (квадрату длины вектора):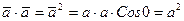 
.
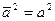3. Переместительное свойство: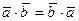 
.
4. Распределительное свойство: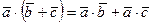 
.
5. Сочетательное свойство: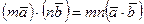 
.
Рассмотренные свойства дают возможность обращаться со скалярным произведением, как с произведением чисел:
.
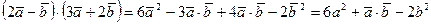6. Скалярное произведение разноименных ортов равно нулю:
.
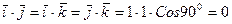Скалярное произведение одноименных ортов равно единице:
.
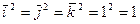7. Если векторы заданы координатами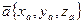 
, 
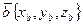, то скалярное произведение равно сумме произведений одноименных координат: 
.
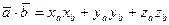Простейшие задачи
1. Косинус угла между векторами определится по формуле:
.
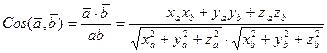2. Проекция вектора на вектор:
.
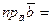
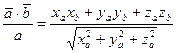3. Условие ортогональности векторов:
.
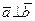
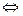
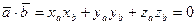Дата добавления: 2015-09-05; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Декартова прямоугольная система координат | | | Векторное произведение двух векторов |