Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Векторное произведение двух векторов и его свойства.

Читайте также:
  1. V. МЫСЛЕННОЕ ВОСПРОИЗВЕДЕНИЕ РИСУНКОВ, КАРТИН, ФОТОГРАФИЙ И Т.П.
  2. XI. ПРИСПОСОБЛЕНИЕ И ДРУГИЕ ЭЛЕМЕНТЫ, СВОЙСТВА. СПОСОБНОСТИ И ДАРОВАНИЯ АРТИСТА
  3. Бесконечно большие и бесконечно малые функции.ихсвойства.примеры.
  4. Векторное произведение векторов.Его геометрический и механический смысл.Перечислить свойства,Векторное произведение в координатной форме.
  5. Векторное произведение двух векторов
  6. Выражение скалярного произведения через координаты векторов

Пусть в пространстве R3 выбрана некоторая прямоугольная система координат OXYZ.

Определение. Векторным произведением вектора а на вектор в называется вектор с = 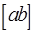,удовлетворяющий следующим трем условиям:

1. Длина вектора с равна произведению длин векторов а и в на синус угла 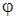между ними, то есть

.

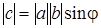Дата добавления: 2015-09-04; просмотров: 41 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Тогда скалярное произведение этих векторов равно сумме произведений соответствующих их координат, то есть| Из определения векторного произведения вытекают следующие его свойства.
mybiblioteka.su - 2015-2024 год. (0.007 сек.)