Из определения векторного произведения вытекают следующие его свойства.

1. = - .

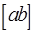2.

3.

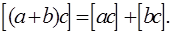
4.

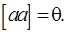
Отметим следующее простое тождество, имеющее место для любых векторов а и в

Теорема. (Выражение векторного произведения через координаты перемножаемых векторов). Пусть трехмерные векторы а и в заданы своими прямоугольными координатами а=(а₁,а₂,а₃), в =(в₁,в₂,в₃). Тогда векторное произведение этих векторов имеет вид:

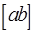= (5)

Дата добавления: 2015-09-04