Тогда скалярное произведение этих векторов равно сумме произведений соответствующих их координат, то есть

ав = а₁в₁+а₂в₂+а₃в₃ (1)

Замечание. Всякий двумерный вектор а = (а₁,а₂) является и трехмерным вектором а = (а₁,а₂,0). Поэтому для двумерных векторов формула (1) имеет вид:

ав = а₁в₁+а₂в₂ (2)

Следствие 1. Угол 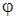между векторами а=(а₁,а₂,а₃) и в=(в₁,в₂,в₃) определяется по формуле

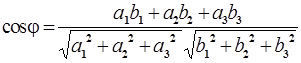(3)

Пример. Вычислить угол между векторами а=(1,0, 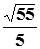) и в=(2,1,0). Формула (3) дает: cos 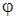= 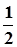. Откуда .

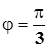Следствие 2. Необходимым и достаточным условием ортого­нальности векторов а=(а₁,а₂,а₃) и в=(в₁,в₂,в₃) является равенство:

а₁в₁+а₂в₂+а₃в₃ = 0 (4)

Дата добавления: 2015-09-04