Скалярное произведение векторов, его свойства.

Текст лекции

Определение. Углом между векторами а и в называется наименьший угол 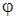, который образуют эти векторы, как стороны, будучи приложенными к общему началу. При 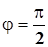векторы называются ортогональными (перпендикулярными).

Определение. Скалярным произведением векторов а и в называется число, равное произведению длин этих векторов на косинус угла между ними:

ав = .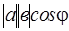

Из определения скалярного произведения вытекают следующие его свойства:

1. ав = ва;

2. а² = аа = ;

3. ( а)в = (ав),

4. (а+в) с = ас+вс;

Дата добавления: 2015-09-04