Декартово (прямое) произведение.

Df1. Декартовым произведением двух множеств А и В называется множество 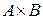, содержащее упорядоченные пары (кортежи), первые компоненты которых принадлежат множеству А, а вторые компоненты – множеству В.

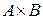= {<a, b>| a A, b B}

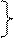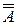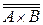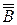Если = n, то = n m

= m

– очевидно

Df2. Декартовым произведением А₁, … А_n, называется выражение

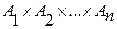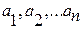= {< >| a₁ A₁, a₂ A₂,… a_n A_n}

Свойства декартового произведения:

1. В отличие от рассмотренных ранее произведений в декартовом произведении не выполняется свойство коммутативности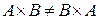

Пример:

А = {1, 2, 3} B = {4, 5}

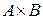= {<1, 4>,<1, 5>,<2, 4 >,<2, 5>,<3, 4>,<3, 5>}

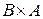= {<4, 1>,<4, 2>,<4, 3 >,<5, 1>,<5, 2>,<5, 3}

2.

3. Если рассматривать n множеств, причем 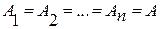, то можно говорить о n-ой степени. Это значит, что берется декартово произведение n одинаковых множеств: 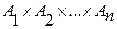= Аⁿ

Дата добавления: 2015-09-01