
Читайте также:
|
Между множествами различают два отношения:
1) Включение (строгое и не строгое).
2) Равенство.
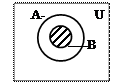
Df1. Множество В включается во множество А, если каждый элемент из множества В входит во множество А: 
 - квантор общности (все, каждый) по переменной х.
- квантор общности (все, каждый) по переменной х.
 | |||
| |||
Df2. Два множества А и В равны (А = В) тогда и только тогда, когда множество А включено во множество В и одновременно множество В включено во множество А.
 1.
1. 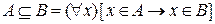
2. 
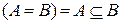 и
и 
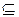 - знак нестрогого включения
- знак нестрогого включения
 - знак строгого включения
- знак строгого включения
 Множество В включено во множество А и не допускает равенства множеств
Множество В включено во множество А и не допускает равенства множеств 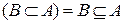 и
и 
Дата добавления: 2015-09-01; просмотров: 57 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Операции над множествами. | | | Основные свойства теоретико-множественных операций. |