График.

Df1. Графиком у при отображении f: А→В называется множество Г_f, состоящее из упорядоченных пар (кортежей) <х, у>, где .

Г {<x, y>| y = f(x), }

  В y_n y = f(x) . пр₂ Г_f . y₁ пр₁ Г_f . А     х₁ ………….х_n A  

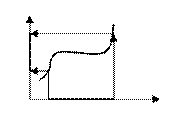
А – 0.0.Г (область определения)

В – 0.3.Г (область значения)

Виды графиков:

1) функциональный,

2) инъективный.

Df2. Функциональным графиком называется график, не содержащий пар с одинаковыми первыми и различными вторыми компонентами.

Df3. Инъективным графиком называется график, не содержащий пар с различными первыми и одинаковыми вторыми компонентами.

Операции над графиками:

В силу того, что график есть множество, то над ним имеют место все теоретико-множественные операции:

Так как график – это упорядоченное множество, то над ним выполняются дополнительные операции:

1) инверсия графика

у {<x, y>| y = f(x), }

у ^-1 {<y, х>| х = f ^-1(у), }

2) композиция двух графиков (), где А и В – графики, называется такой третий график С, который определяется следующим образом

= С

Дата добавления: 2015-09-01