

 Разбиение – есть операция над множествами.
Разбиение – есть операция над множествами.

По одному свойству универсальное множество делится (разбивается) на два подмножества А и  , обладающие такими свойствами:
, обладающие такими свойствами:
1) А  =
=  , 2) А
, 2) А  = U
= U
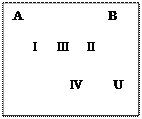
Возьмем два свойства: Р(х), Q(х). Тогда универсум U разбивается на 4 подмножества:
I, II, III, IV.
 А = {х
А = {х  U | P(х)} - I
U | P(х)} - I
 В = {х
В = {х  U | Q(х)} - II
U | Q(х)} - II
А 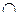 В = {х
В = {х  U | P(х) и Q(х)} - III
U | P(х) и Q(х)} - III
U\(А 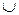 В) = {х
В) = {х  U |
U | 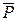 (х) и
(х) и  (х)} - IV
(х)} - IV
1) 
2) 
Если P1, P2,…, Pn свойства, то по этим n свойствам разбиваем множество U на 2n частей.
1.  ,
,  ; i, j
; i, j 
2.  .
.
Операции над множествами, удовлетворяющими свойствам 1 и 2, называются разбиением множеств. Части множеств Ki называются классами.
Дата добавления: 2015-09-01; просмотров: 42 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Доказательство тождеств в алгебре множеств. | | | Кортеж (вектор). |