Отображение.

Возьмем два множества А, В

Рассмотрим как могут соотносится эти два множества

Df1. Отображением множества А во множество В называется такое соответствие двух множеств А и В, при котором каждому элементу множества А сопоставляется точно один элемент множества В.

f: А В – отображение А в В.

Г_В(А) – отображение А в В: y = f(x), где х А y В.

В такой записи х называется прообразом, у – образом.

f: А = В

Виды отображений:

1. Сюръекция (отображение на) отображение А на В.

Df2. Если каждому элементу из множества В сопоставляется хотя бы одинэлемент из множества А, то такое отображение f: А В называется сюръекцией (или отображением множества А на множество В)

2. Инъекция («впрыскивание»).

Df3. Если каждому элементу из множества В сопоставляется не более одного элемента из множества А, то такое отображение f: А 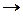В называется инъекцией.

3. Биекция.

Df4. Если каждому элементу из множества В сопоставляется точно один элемент из множества А, то такое отображение f: А 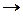В называется биекцией.

Биекция есть очевидно одновременно отображение сюръективное и инъективное. Биекция используется для определения мощности в силу установления одно-однозначного отображения двух множеств. Если множества А и В имеют одинаковое число элементов, то между ними устанавливается биективное отображение. Такие множества называются равночисленными. Если А и В – бесконечные множества и между ними устанавливается биективное отображение, то такие множества называются равномощными.

A = N = {1, 2, 3…}

B = N_чет = {2, 4, 6…}

f: n 2n, где n A, 2n B => биекция – мощности равны (парадокс).

Парадоксы, когда часть множества равна целому, могут встречаться только если множества бесконечные.

Df5. Если множества А и В связаны инъективным (биективным) отображением, то они называются эквивалентными (А~В).

Свойства эквивалентности множеств (А~В):

1) рефлексивность: А~А,

2) симметричность: А~В В~А,

3) транзитивность: А~В, В~С → А~С.

Для того, чтобы определить счетно ли множество необходимо установить, что оно биективно или эквивалентно множеству N.

Свойства отображений:

Если f: x→y, то говорят, что f ^-1: х←у – это отображение называется обратным, при

этом два множества (А, В)связаны средством включения:

1) ,

2) ,

3) .

Дата добавления: 2015-09-01