Соответствие.

Df1. Соответствие Г называют тройку множеств <G, X, Y>, где 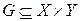- график.

Х – область отправления, Y – область прибытия

Пример:

Х {a, b, c} a b c

график соответствия Г

Y { } α β γ

пр₁ Г = { }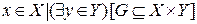

пр₂ Г = { }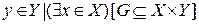

пр₂ Г – берутся элементы Y такие, что для всех х существует пара, соответствующая условию

<x, y>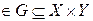

Поскольку основным свойством соответствия является подмножество G декартового произведения, то все ранее рассмотренные свойства графиков относятся и к свойствам соответствия.

Основные свойства соответствий:

1. а) Соответствие имеет вид 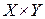- полное множество.

Г 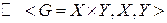(полное соответствие).

б) Г 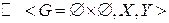- не берем ни одного элемента из множеств X и Y. Г – пустое соответствие. Все остальные графики лежат между этими двумя.

2. Над соответствием можно выполнять инверсию:

Г ^-1 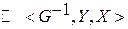, где Y – область отправления, X – область прибытия.

Для выполнения инверсии достаточно, например:

Х {a, b, c} a b c

График

Y { } α β γ

Х {a, b, c} a b c

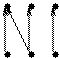Инверсия

Y { 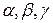} α β γ

Достаточно стрелки направить в обратном направлении Г(х = пр₁ G) пр₂
G = у.

3. Композиция соответствия. Имеет смысл для двух и более соответствий.

Рассмотрим для двух соответствий

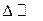<H, V, W> 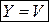- основное условие

Г <G, X, Y>

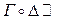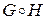< , X, W>

Заданы 2 соответствия, требуется найти их композицию. Прежде чем находить композицию необходимо в первую очередь проверить равенство области прибытия Y, области отправления V.

4. Под Г(А) понимают множество элементов из области, для которого существует 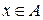из заданного графика.

Г(А) { }

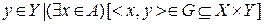Полный образ множества А при соответствии Г.

5. Если А есть подмножество В, если над ними взять одинаковые соответствия, то Г(А) будет вложено в Г(В).

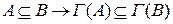
Например, Г(А) = , то вновь введенное множество А и пр₁G не пересекутся.

Г(А) = А пр₁G = .

Х {a, b, c} - пр₁G a b c

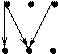
Y { 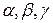} – пр₂G α β γ

Пусть А = Х Г(Х = пр₁G) пр₂G = Y

Cужение соответствия:

Между Г(А) = и Г(А=Х) = Y лежат все остальные

Г_А – сужение соответствия Г на множество А.

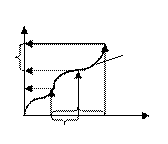Чтобы взять сужения соответствия Г нужно взять график и его урезать, т.е. взять из него такие элементы соответствующие .

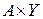Сужение соответствия Г определяется через сужение графика данного соответствия.

Г_А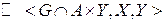

В двойственном определенном смысле есть понятие продолжения соответствия.

Г_В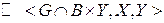

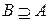
Прообраз соответствия:

Г^-1(А)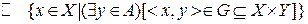

Элементы множества А – элементы области прибытия

Свойства прообразов соответствия:

1. ,

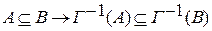2. .

, .

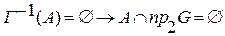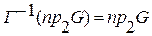Поскольку соответствие задается не только в виде графика, это есть некоторое отображение множества Х на множество Y, которое задается в виде графика Y, т.е. смысл говорить о соответствии как об отображении. Соответствия как и отображения могут быть сюрьективным, биективным и инъективным.

Соответствие Г является:

1) функциональным, если

Г <G, X, Y> - G – функциональный.

2) инъективным, если G – инъективный.

3) всюду определенным, если график G всюду определен.

4) сюрьективное, если график G: 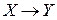сюрьективный (отображение на).

5) взаимнооднозначное (биективное), если график G: 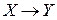- биективный (во-первых, Г всюду определено, во-вторых, оно и функциональное и инъективное, в-третих, является сюрьективным).

Дата добавления: 2015-09-01