
|
Читайте также: |

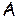 = {M;
= {M; 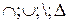 }, где М
}, где М 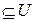 ,
, 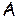 алгебра множеств.
алгебра множеств. 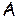 (а готическое рукописное).
(а готическое рукописное).
объекты операции
В алгебре множеств рассматриваются основные тождества и свойства этих тождеств. Рассматриваются уравнения двух типов
1) U(A, B, C…) = B(A, B, C…) множества заданы подмножествами А, В, С…
2) U(А, В, С…) = 0
Докажем эти тождества. Существует 3 метода доказательства тождеств:
1. геометрический,
2. аналитический (с использованием понятия эвристики),
3. аналитический (с использованием основных свойств теоретико-множественных операций).
Рассмотрим геометрический метод доказательства для первого тождества на примере:
U(A, B, C…) = B(A, B, C…)
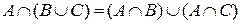


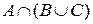
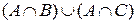
Картинки аудентичны (доподлинно одинаковы по построению)
Преимущество геометрического метода: наглядность.
Недостаток: при большом количестве множеств, участвующих в построении (более 5), теряется наглядность данного метода.
Аналитический метод исправляет недостаток геометрического метода, но сам он не наглядный.
U(A, B, C…) = B(A, B, C…)
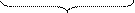
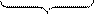
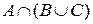 =
= 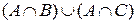
D F
 1) (А = В) = А
1) (А = В) = А 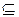 В и В
В и В 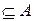
2) (А 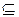 В) = (
В) = (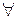 х) [х
х) [х  А
А  х
х  В] условия равенства двух множеств
В] условия равенства двух множеств
3) (В 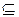 А) = (
А) = (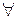 х) [х
х) [х  В
В  х
х  А]
А]
(D = F) = D 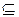 F и F
F и F 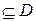
(D 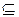 F) = (
F) = (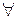 х) [х
х) [х  D
D  х
х  F]
F]
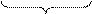 x
x  D = x
D = x  A
A 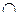 (B
(B 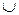 C) =
C) =
D
по свойству теоретико-множественных операций переходим к более простому виду записи:
= x  A и x
A и x  A
A 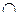 (B
(B 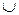 C) = x
C) = x  A и [x
A и [x  В или x
В или x  С] =
С] =
Сейчас мы должны перейти к методам эвристики. Эвристический путь сокращает перебор решений. При эвристическом пути рассуждать необходимо после рассмотрения левой части доказываемого множества (рассмотрение до уровня разложения на элементы отношения принадлежности и простейшие логические союзы (и, или)) перейти к рассмотрению таким же образом правой части.
= (x  A и x
A и x  В) или (x
В) или (x  A и x
A и x  С).
С).
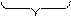 | |||
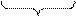 | |||
= [x  (A
(A 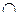 В)] или [x
В)] или [x  (A
(A 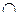 С)] = x
С)] = x  [(A
[(A 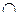 В)
В) 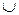 (A
(A 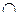 С)]
С)]
 |
F
Взяв х – произвольный элемент во множестве D, мы обнаружили его во множестве F.
Аналогичным образом докажем: (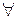 х) [х
х) [х  F
F  х
х  D] = F
D] = F 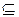 D и получим конечный результат: (D = F) = D
D и получим конечный результат: (D = F) = D 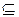 F и F
F и F 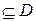 .
.
 |
Рассмотрим 3-й метод для второго вида тождеств:
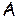 (A,B,C,…)=0;
(A,B,C,…)=0;
А\[(А 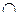 В)
В) 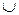 (А\В)] =
(А\В)] = 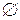
По свойству дистрибутивности исходное тождество можно переписать следующим образом:
А\{[А 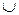 (А\В)]
(А\В)] 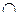 [В
[В 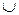 (А\В)]} = А\{А
(А\В)]} = А\{А 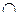 (А
(А 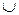 В)} = А\А =
В)} = А\А = 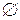
 |  | ||
А А  В
В
Этот метод наиболее продуктивен, но требует знания основных свойств теоретико-множественных операций и умении пользоваться диаграммами Эйлера-Венна.
Дата добавления: 2015-09-01; просмотров: 143 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные свойства теоретико-множественных операций. | | | Разбиение. |