
Df1. Отношением  называют пару множеств
называют пару множеств 
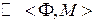 , где
, где 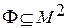
Рассматривают или имеют место отношения на некотором множестве М, а не просто отношение.
Пример:
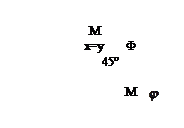
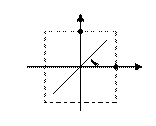 М – множество элементов числовой оси
М – множество элементов числовой оси
Ф: х = у
М2 – декартовый квадрат М2 = М 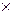 М
М
 - связывает элементы х и у
- связывает элементы х и у
х  у, через
у, через  (=, >, <…)
(=, >, <…)
можно обозначить любое взаимное отношение между двумя элементами:
х = у, х || у, х 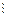 у, х
у, х  у, х > у, х
у, х > у, х 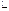 у, и т.д.
у, и т.д.
Операции над отношениями:
1. Полное отношение

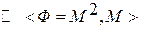
2. Пустое отношение

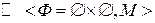 , Ф черпает элементы из множества М.
, Ф черпает элементы из множества М.
3. Диагональное отношение
ЕМ 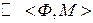 , где <х, у>
, где <х, у>  Ф, х = у.
Ф, х = у.
Над отношениями имеют место операции как над множествами, поскольку отношения – это множества (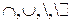 )
)
1) Рассмотрим операцию 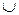

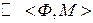 , где Ф
, где Ф 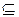 М2
М2
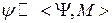 , где
, где  М2
М2
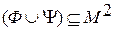
 , где
, где 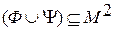
Пример:
хφу х = у
хψу х > у
 х(φ
х(φ 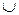 ψ)у| х(=
ψ)у| х(= 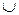 >)у = х
>)у = х  у
у
2) Рассмотрим операцию 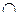

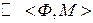 , где Ф
, где Ф 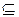 М2
М2
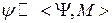 , где
, где  М2
М2
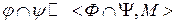 , где
, где 
3) Заданы 2 отношения φ и ψ, нужно найти их разность
 , где
, где 
4) 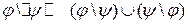
5) Дополнение
Имеется некоторое отношение 
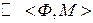 , где Ф
, где Ф 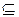 М2
М2
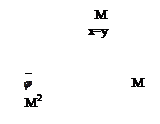
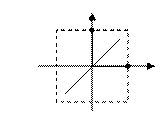

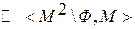
 - дополнение отношения φ, получается путем изъятия из декартового квадрата множества точек графика
- дополнение отношения φ, получается путем изъятия из декартового квадрата множества точек графика
Рассмотрим операции над отношением, как над графиком
1. Инверсия:
 -1
-1 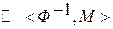 , где Ф-1
, где Ф-1 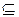 М2
М2
2. Композиция:

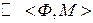 , где Ф
, где Ф 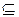 М2
М2

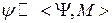 , где
, где  М2
М2

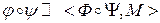 , где
, где 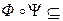 М2
М2
x, y, z  М
М
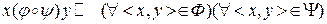
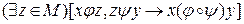
3. Импликация
Если рассматривать 2 отношения, связанные следующим образом 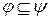

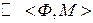 , где Ф
, где Ф 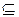 М2
М2
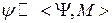 , где
, где  М2,
М2,
то говорят, что φ имплицирует ψ, если задав пару отношением φ находим такую же пару в отношении ψ, т.е. 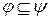 (
(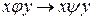 )
)
4. Сужение
Если задано отношение φ, то попытаемся сузить на множество А.
φА – сужение отношения φ на множество А
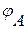

Отношение эквивалентности
 - задано отношение, оно называется эквивалентностью, если удовлетворяет следующим условиям:
- задано отношение, оно называется эквивалентностью, если удовлетворяет следующим условиям:
1) Рефлексивность: х  х
х
а) 
 =, х = х
=, х = х
б) 
 >, х>х
>, х>х
2) Симметричность: х  у→у
у→у  х
х
а) 
 = х = у→у = х
= х = у→у = х
б) 
 > х > у
> х > у 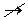 у > х
у > х
3) Транзитивность: 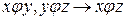
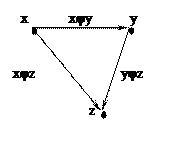
Если удовлетворяет этим условиям, то говорят, что φ 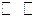 (эквивалентность).
(эквивалентность).
Отношение эквивалентности собирает вокруг себя элементы одного класса.
х~y
|

|
| ……………. |
| …………… |
|


Классы обладают свойством собирать вокруг себя элементы, удовлетворяющие эквивалентности. С другой стороны между классами нельзя взять пару элементов, удовлетворяющих эквивалентности.
Отношение φ 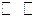 разбивает исходное множество М на классы. Легко видеть, что
разбивает исходное множество М на классы. Легко видеть, что
а)  , б)
, б) 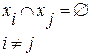
Берем исходное множество М – фактор-множества: это множество М, разбитое на классы отношением φ.
Пример:
Студенты факультета разбиты на курсы. Внутри курса 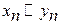 , но
, но 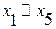 , т.е нельзя приравнять первокурсника к пятикурснику.
, т.е нельзя приравнять первокурсника к пятикурснику.
Некоторые дополнительные свойства отношений:
Пусть задано отношение 
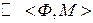 , где Ф
, где Ф 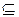 М2
М2
1) Рефлексивность: 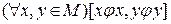
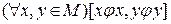
2) Симметричность: 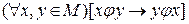
3) Транзитивность: 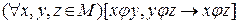
4) Антисимметричность: 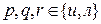
5) Связанность или связность: 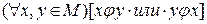
Отношения типа порядка простейшие отношения >, <
Квазипорядок – якобы порядок, не отвечает свойству рефлексивности.
Дата добавления: 2015-09-01; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Соответствие. | | | Высказывания. |