
|
Читайте также: |
Df1. Высказывание – это повествовательное выражение, относительно которого можно сказать истинно оно или ложно.
Df2. Высказывательная форма
Р(х1,…, xn) – это предложение, которое обращается в конкретное высказывание при подстановке вместо (х1,…, xn) конкретных значений
(х1,…, xn) – высказывательные переменные
Пример:
Р(х)  ”х делится на 2”,
”х делится на 2”,
Различают высказывания простые и сложные
Сложные высказывания образуются из простых или так называемых атомарных с помощью следующих союзов.
Логические союзы:
1. не ( )
)
2. и (&)
3. или (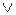 )
)
4. если…, то…(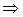 )
)
5. …тогда и только тогда, когда…(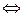 )
)
Df3. Отрицание – есть сложное высказывание, образованное из исходного с помощью частицы «не».
Пример:
1) Р(х)  «в аудитории №5 была собачка»
«в аудитории №5 была собачка»
2)  Р(х)
Р(х)  «в аудитории №5 не было собачки» - сложное высказывание относительно 1
«в аудитории №5 не было собачки» - сложное высказывание относительно 1
Высказывания обозначаются A, B, C, D…, иногда разрешается p, q, z…
| Р | Q |  P P
| P&Q | P 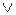 Q Q
| P→Q | P 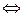 Q Q
|
| И Л И Л | И И Л Л | Л И Л И | И Л Л Л | И И И Л | И И Л И | И Л Л И |
Р(х)  {И, Л}
{И, Л}
Таблица истинности
Df4. Конъюнкцией (логическое произведение) двух высказываний P и Q называют третье сложное высказывание (P&Q), образованное из простых высказываний P и Q с помощью союза «и», принимающее значение истинно при одновременной истинности составляющих высказываний, значение ложно – при всех остальных.
Df5. Дизъюнкцией (логическое сложение) двух высказываний P и Q называют третье сложное высказывание (P 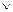 Q), которое принимает истинное значение при истинности одного из исходных высказываний P или Q и ложное значение при одновременной ложности исходных высказываний.
Q), которое принимает истинное значение при истинности одного из исходных высказываний P или Q и ложное значение при одновременной ложности исходных высказываний.
Df6. Импликацией (логическое следование) двух высказываний P и Q называется третье высказывание (P→Q, P 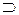 Q, P
Q, P 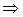 Q), которое принимает ложное значение при истинности значения Р и ложности Q, при всех остальных ситуациях принимает истинное значение.
Q), которое принимает ложное значение при истинности значения Р и ложности Q, при всех остальных ситуациях принимает истинное значение.
Df7. Эквиваленция (логическая равнозначность) двух высказываний P и Q, обозначается (P~Q, P 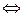 Q), которое принимает истинное значение при совпадающих значениях исходных высказываний и ложное значение при различных значениях P и Q.
Q), которое принимает истинное значение при совпадающих значениях исходных высказываний и ложное значение при различных значениях P и Q.
Примеры сложных высказываний:
1) Сегодня на лекции присутствуют все студенты (Р)
2) Сегодня не все студенты присутствуют на лекции (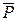 )
)
3) На лекции студенты слушают (P) и конспектируют (Q)
Структура высказывания: P&Q.
4) На лекции студенты слушают (P) или разговаривают (Q)
Структура высказывания: P 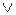 Q.
Q.
5) Если студенты посещают занятия (P), то они успешно смогут сдать экзамены (Q)
Структура высказывания: P→Q.
6) Студенты смогут успешно сдать экзамены (P) тогда и только тогда, когда они выполняют весь учебный план (Q)
Структура высказывания: P~Q.
Переход от посылки к заключению P→Q называется выводом. Если посылка была истинной, а заключение – ложным, то вывод был ложным.
Из ложности посылки можно получить ложный и истинный результат.
С помощью логических союзов образуются сложные высказывания путем выполнения каких-то операций, их принято называть логическими (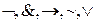 )
)
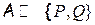 - алгебра логики, где P – множество логических переменных, принимающих значения либо И либо Л. Q – множествологическихопераций.
- алгебра логики, где P – множество логических переменных, принимающих значения либо И либо Л. Q – множествологическихопераций. 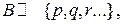 где
где 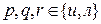
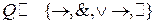 кроме того применяются скобки: (,), [, ].
кроме того применяются скобки: (,), [, ].
Дата добавления: 2015-09-01; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Отношение. | | | Свойства логических операций. |