Векторное произведение двух векторов

Правой связкой трех некомпланарных векторов 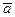, , 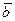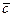(взятых в таком порядке) с общим началом в точке О (рис. 11) называется такое их расположение, когда кратчайший поворот первого вектора до совмещения со вторым смотрится с конца третьего вектора происходящим против хода часовой стрелки. В противном случае имеем левую связку векторов 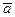, , 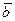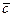(рис. 12).

Рис. 11 Рис. 12

Векторным произведением двух векторов 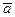и 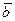называется новый вектор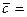 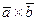, такой, что

1. ;

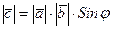2. 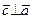и ;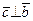

3. 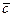направлен так, что связка векторов 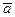, , 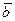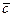- правая.

Здесь знак умножения крестиком – знак векторного умножения векторов.

Свойства векторного произведения:

1. Векторное произведение равно нулю тогда и только тогда, когда вектора 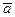и 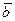коллинеарны: || .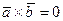

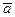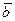2. .

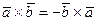Таким образом, переместительный закон для векторного произведения не выполняется.

3. Распределительное свойство: .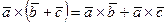

4. Сочетательное свойство: .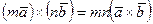

5. Векторное произведение одноименных ортов равно нулю:

.

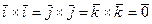Векторное произведение разноименных ортов определяется следующей таблицей, 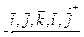из которой видно, что 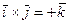, , 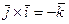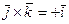и т.д.

6. Векторное произведение в координатной форме есть определитель третьего прядка, у которого первая строка – координатные орты, вторая строка – координаты первого вектора-сомножителя, третья строка – координаты второго вектора-сомножителя: .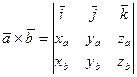

Простейшие задачи

1. Площадь параллелограмма, построенного на векторах 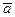и :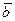

| |= | |.

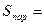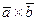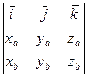2. Площадь треугольника, построенного на векторах 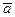и :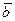

.

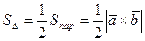Дата добавления: 2015-09-05