Читайте также:
|
 |
, 
, 
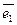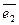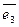и точки О – начала координат (affinis – смежный, соседний).
Рис. 4
Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат: первая – ось абсцисс; вторая – ось ординат; третья – ось аппликат. Плоскости, проходящие через оси координат – координатные плоскости.
Пусть в пространстве задана точка М.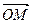 
- радиус-вектор точки М. Тогда разложение по векторам базиса = 
+ 
+ 
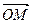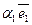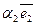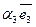. Аффинными координатами точки М называются координаты - радиус-вектора
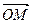в рассматриваемой системе координат, пишут 
, где 
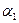- абсцисса, 
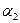- ордината, 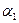- аппликата точки М. В заданной аффинной системе координат координаты фиксированной точки определяются однозначно. С другой стороны, если задана система координат, то в ней каждой упорядоченной тройке чисел ставится в соответствие единственная точка. Аффинная система координат на плоскости 
определяет такое же соответствие между точками и упорядоченными парами чисел.
 |
и 
. Требуется найти координаты вектора 
.
Рис. 5
Р е ш е н и е. Из чертежа (рис. 5) видно 
, тогда
+ 
+ 
+ + 
=
= 
.
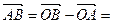
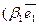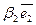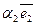Таким образом, 
, то есть, координаты вектора равны разности соответствующих координат конца и начала вектора.
Дата добавления: 2015-09-05; просмотров: 84 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Разложение вектора по базису | | | Проекция вектора на ось |