Задача 4.1. определить прямоугольные координаты вершин треугольника.

Для решения задачи каждому студенту необходимо иметь ксерокопию карты, на которой преподаватель наносит вершины треугольника АВС. Прежде чем приступить к решению задачи необходимо определить масштаб карты и разобраться с оцифровкой сетки координат. Затем выделить квадрат километровой сетки, в которой находится вершина треугольника и выписать координаты его юго-западного угла. На рис. 11 для точки А Х =6068 км, Y =4312 км (напоминаем, что первая цифра у ординаты означает номер зоны, в которой находится данная карта).

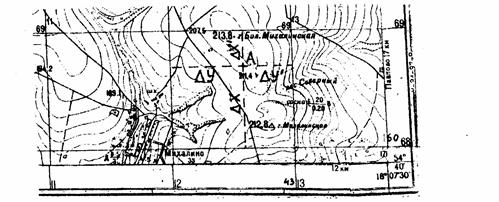
Рис. 11. Схема определения прямоугольных координат на топографической карте

Из точки А опускают перпендикуляры на стороны квадрата километровой сетки. С помощью измерителя и масштабной линейки определяют длины перпендикуляров относительно южной и западной стороны квадрата. То есть измеряют приращения координат. Тогда значения координат точки А будут равны:

XA=X ю.з.+ ∆ X A (4)

YA = Y ю.з..+ ∆ Y A (5)

Недостатком изложенного способа является его бесконтрольность. Здесь любая грубая ошибка в измерении остается незамеченной. Поэтому на практике измеряют не только отрезки ∆ Х А и ∆ Y A, но и продолжения их до северной и восточной сторон километровой сетки, т.е., ∆ Х А´ и ∆ Y A´. Очевидно, что при отсутствии погрешностей в измерениях должны выполнятся условия:

∆ X A +∆ Х А´= D (6)

∆ Y A+∆ Y A´= D, (7)

где D – длина стороны квадрата километровой сетки (1км).

Практически таких равенств не получается из-за случайных и систематических погрешностей измерений (деформация бумаги, не точность установки игл измерителей в вершины, погрешности построения поперечного масштаба и т.д.). Однако величина неравенства не должна превышать 0.3мм в масштабе карты. Если это условие выполняется, то окончательные координаты точки А можно вычислить по формулам.

X A= X ю.з+(D /(∆ X A +∆ Х А´))∆ X A, (8)

Y A= Y ю.з+(D /(∆ Y A +∆ Y B´))∆ Y A. (9).

Данные формулы и рекомендуется использовать при решении задачи 4.1. результаты измерений записывают в таблицы 2 и 3.

Однако такой контроль не всегда осуществим. Например, в таблице 2 отрезок ∆ Х А´

отсутствует, так как линия координатной сетки 6069 находится на соседнем листе карты. В таких случаях наиболее действенным контролем является вычисление длины отрезка dAB и сравнение его с непосредственно измеренной длиной этого отрезка по карте. Это поможет избежать грубой погрешности определения координат.

В таблицах 2 и 3 приведены результаты измерения координат вершин треугольника АВС (см. Приложение 1).

Таблица2 Абсциссы точек А, В,С. (км)

Точка	X ю.з (км)	∆ X (км)	∆ Х´ (км)	Х (км)
А		0.356		6068.356
В		0.582	0.413	6067.585
С		0.451	0.545	6067.453

Таблица 3Ординаты точек А,В,С (км)

Дата добавления: 2015-09-01