Система плоских прямоугольных координат Гаусса-Крюгера

При картографировании значительных частей земной поверхности с целью перехода от сферы к плоскости применяют различные картографические проекции. Дело в том, что сферическую поверхность развернуть в плоскость без разрывов невозможно. Поэтому любая картографическая проекция имеет искажения. Их величина зависит от вида проекции. Так в равноугольных проекциях сохраняется подобие углов, но искажаются длины линий; в равновеликих не искажаются площади, в равнопромежуточных – не искажаются длины линий по какому-либо направлению (по меридиану, параллели) и т.д.

Для целей крупномасштабного картографирования, то есть для составления топографических карт, применяют равноугольную поперечно-цилиндрическую проекцию Гаусса-Крюгера. В этой проекции сохраняются подобие изображения фигур при переходе с эллипсоида на плоскость, а искажение длин линий не выходит за пределы графической точности.

Геометрический смысл этой проекции заключается в следующем. Поверхность сферы разбивают меридианами через 6 градусов на зоны, каждая из которых отдельно проецируется на боковую поверхность цилиндра (рис 9). Разрезав цилиндр по образующей, проходящей через земные полюса, получают изображение сферической поверхности на плоскости (рис 10).

На полученном изображении осевой меридиан зоны (меридиан касания зоны и цилиндра) и экватор,- взаимно перпендикулярные прямые линии, а остальные меридианы и параллели – кривые. Искажения размеров длин линий в близи осевого меридиана минимальные и возрастают по мере удаления к краям. Линия на поверхности шара длиной D при изображении ее на плоскости получит искажение ∆ D, которое можно вычислить по формуле:

∆ D = Y²mD/2R ², (3)

где Ym=(Y1+Y2) /2 – среднее значение из ординат начальной и конечной точек линии;

R – радиус Земли.

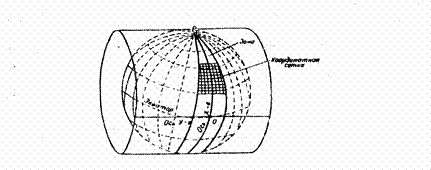
Рис.9. Схема образования равноугольной поперечно – цилиндрической проекции Гаусса – Крюгера

Относительные искажения ∆ D/D на краях шестиградусной зонымогут достигать величины порядка 1/1500, а трехградусной – 1/6000. Выбор ширины зоны зависит от требований, предъявляемых к точности топографической карты. Если для проектирования нужны карты масштаба 1:10 000 и мельче, то применяют шестиградусные зоны, для более крупных масштабов – трехградусные.

В каждой зоне, а их 60, задаётся своя система прямоугольных координат, в которой за ось абсцисс (Х) принимается осевой меридиан, а за ось ординат (Y) – экватор

(рис 10).

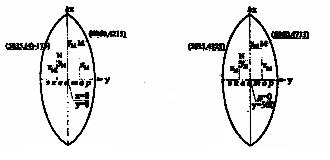
а) непреобразованная б)преобразованная

Рис. 10. Система плоских прямоугольных координат Гаусса – Крюгера

Зоны нумеруются арабскими цифрами с запада на восток, начиная от Гринвичского меридиана. Для удобства измерения прямоугольных координат на карте проводят сетку, состоящую из прямых линий, параллельных осевому меридиану и экватору, которая называется координатной. Расстояние между смежными линиями сетки для масштабов карт 1:10 000, 1:25 000, 1:50 000 составляет 1 км на местности. У западной и восточной рамок карты подписывают абсциссы, а у северной и южной - ординаты координатной сетки. Они позволяют легко определить прямоугольные координаты любой точки, изображенной на карте.

Для территории нашей страны расположенной в северном полушарии, абсциссы всегда положительны и их величина соответствует расстоянию от экватора до данной линии. Для того, чтобы и ординаты были всегда положительными, их начало смещают на запад на 500 км.

Дата добавления: 2015-09-01