Задача 5.2. Измерить с помощью транспортира прямые и обратные дирекционные углы линий АВ,ВС,СА. Вычислить значения их румбов и внутренних углов треугольника.

Как уже отмечалось, одним из существенных недостатков истинных азимутов и румбов, как углов ориентирования, является их зависимость от широты точки, в которой измеряется угол, а также неравенство прямого и обратного угла. Поэтому на практике более широкое распространение получили углы ориентирования, называемые дирекционными углами α

Угол, отсчитываемый от северного направления осевого меридиана или линии параллельной ему по ходу часовой стрелки до направления данной линии, называется дирекционным углом. Прямой и обратный дирекционные углы отличаются ровно на 180° Дирекционные углы отличаются от азимутов на величину гауссова сближения меридианов γг. Применительно к проекции Гаусса – Крюгера формула вычисления γг имеет вид

γг= (L-L0)sinB, (12)

гдеL – долгота меридиана в определяемой точке,

L0 – долготаосевого меридиана данной зоны. Номер зоны всегда подписан первой цифрой перед значением координаты Y. Например, для зоны с номером 4, долгота осевого меридиана равна 21⁰.

Гауссово сближение меридианов может быть восточным или западным в зависимости от положения точки относительно осевого меридиана. Для восточной половины зоны сближение меридианов считается положительным, для западной – отрицательным. На топографической карте ниже южной рамки всегда указывается гауссово сближение меридианов для средней части листа.

В практике, кроме непосредственно измеренных углов ориентирования, часто используют их производные – румбы (рис.13). Дирекционным р умбом линии называется угол между ближайшим (северным или южным) направлением осевого меридиана и заданной линией. Чтобы различить, какое направление относительно сторон горизонта имеет данная линия, перед градусной величиной румба указывают название соответствующей четверти. Например: СВ: 45°00´, ЮЗ: 15°00´ и т.д.

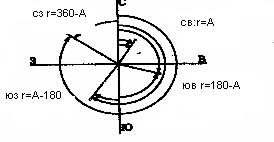
Рис.13. Связь между дирекционными углами и румбами

Используя связь между румбами и основными углами ориентирования по рис.13 или таблице 6 легко перейти от дирекционных углов к их румбам и наоборот.

Таблица 6.Связь между румбами и дирекционными углами

Номер четверти	Название румба	Значение Дирекционного угла, α	Значение румба, r
।	СВ	0°-90°	r =α
॥	ЮВ	90°-180°	r =180°-α
।।।	ЮЗ	180°-270°	r =α-180°
।Y	СЗ	270°-360°	r =360°-α

Так как дирекционный угол – это угол между северным направлением осевого меридиана и направлением заданной линии, измеренный по ходу часовой стрелки, то решение первой части задачи сводится к измерению угла между вертикальной линией сетки (осью абсцисс) и заданной линией. Результаты измерений следует записать в табл.8. В качестве примера в ней переведены результаты измерений дирекционных углов сторон треугольника АВС приложения 1.

Таблица 8.Результаты измерения дирекционных углов сторон треугольника АВС

Название линий	Дирекционные углы α	Румбы, r	Углы
АВ	131°15´	юв:48°45´	ÐА=58°30´
ВС	262°45´	юз:82°45´
СА	9°15´	св:9°15´	ÐВ=48°30´
ВА	311°15´	сз:48°45´
СВ	83°00´	св:83°00´	ÐС=73°45´
АС	189°45´	юз:9°45´	∑=180°15´

Дирекционные углы можно не только непосредственно измерить на карте, но и вычислить по формуле 13, если известны координаты концов отрезка, т.е X _А Y _А X _В Y _В. Однако следует иметь в виду что по этой формуле всегда будем иметь румб линии.

tg r AB=(Y В- Y А)/(X В- X А). (13)

Для перехода от румба к дирекционному углу необходимо установить название четверти, в которой он находится, ориентируясь на знаки приращений координат (YВ-YА) и (XВ-XА) в соответствии с табл.9, а уже затем вычислить искомый дирекционный угол, используя связь между дирекционными углами и их румбами по табл.6 или рис.13.

Таблица 9. Знаки приращений координат в зависимости от четверти румба

Разности координат	СВ	ЮВ	ЮЗ	СЗ
Y В- Y А	+	+	-	-
X В- X А	+	-	-	+

Задача 5.3. Вычислить дирекционные углы сторон АВ,ВС,СА по формуле 13, используя прямоугольные координаты, полученные в задаче 4.1 и сравнить их с измеренными (табл.8). дать анализ причин расхождений между вычисленными измеренными величинами.

Таблица 10.Результаты сравнения вычисленных и измеренных дирекционных углов

Название линий	Вычисленные румбы, r	Вычисленные дирекционные углы, αвыч	Измеренные дирекционные углы,αизм	Расхождение αвыч -- αизм
АВ	юв: 49°17´	130°43´	131°15´	-0°32´
ВС	юз: 82°47´	262°47 ´	262°45 ´	0°02´
СА	св: 9°11´	9°11´	9°15 ´	-0°04´
ВА	сз: 49°17´	310°43 ´	311°15 ´	-0°32´
СВ	св: 82°47´	82°47 ´	83°00 ´	-0°13´
АС	юз: 9°11´	189°11 ´	189°45 ´	-0°34´

Задача 5.4. Найти сближение меридианов как разность между географическим азимутом и дирекционным углом и сравнить его с вычисленным по формуле 12 для точек А,В,С. Дать анализ причин расхождений. γизм и γвыч. (для любознательных)

Таблица 11. Вычисление сближений меридианов

Название сторон	Истинные азимуты Аизм	Дирекционные углы, α изм	Сближение γизм	меридианов γвыч
АВ	128°00´	131°15´	-2°45´	-2°23´23´´
ВС	260°15´	262°45´	-2°30´	-2°22´41´´
СА	6°30´	9°15´	-2°45´	-2°23´26´´

Задача 5.5. Вычислить магнитные азимуты линий АВ,ВС,СА, используя значения дирекционных углов (табл.8), а склонение магнитной стрелки и сближение меридианов взять из приложения 2 по заданному преподавателем варианту. Решение задачи иллюстрировать рисунками. (для любознательных)

Ориентирование линий относительно магнитного меридиана является наиболее простым в практическом исполнении, так как положение магнитного меридиана на местности даёт направление магнитной стрелки. Но такого рода ориентирование не находит широкого применения в массовых геодезических работах и особенно на строительной площадке. Это обусловлено изменением величины склонения магнитной стрелки в зависимости от места и времени. Так, на Европейской части России, восточное склонение колеблется от 0° (в районе Калининграда) до 20° (в районе Нарьян-Мара).

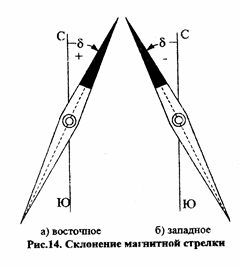Склонение магнитной стрелки есть угол между северными направлениями истинного и магнитного меридиана (рис.14).

Cклонение магнитной стрелки может быть восточным и западным. Восточному склонению приписывают знак (+), а западному (-). Это обусловлено положением магнитного меридиана относительно географического (истинного). Склонение претерпевает вековые, годовые и суточные изменения.

Вековые изменения склонения продолжительностью около четырех веков имеют амплитуду в несколько десятков градусов. Амплитуда годовых колебаний в Европейской части России в отдельных местах достигает 5°, а суточная - 15´. При этом изменение не имеют математически выраженных закономерностей, поэтому учет их представляет определенные трудности.

Кроме того, величина склонения изменяет свое значение под влиянием магнитных возмущений и магнитных бурь, связанных с полярным сиянием, солнечной активностью. В районах магнитной аномалии, а также вблизи линий электропередач положение магнитного меридиана становится неопределенным.

Все отмеченное выше не позволяет нанести на карту линии магнитных меридианов, а следовательно и измерить по карте магнитный азимут. В тоже время ниже южной рамки топографической карты всегда указывается склонение магнитной стрелки (δ) на дату составления карты, а также годовое изменение склонения. Это позволяет вычислить величину склонения на текущее время, а следовательно и значения истинного азимута.

Ориентирование по магнитному меридиану находит широкое применение в лесоустроительных работах и при картографировании небольших участков земной поверхности (менее 1км²) в труднодоступных районах. В этих случаях возникает необходимость перехода от измеренных дирекционных углов или истинных азимутов к магнитным азимутам линий. Связь между ними показана на рис.15.

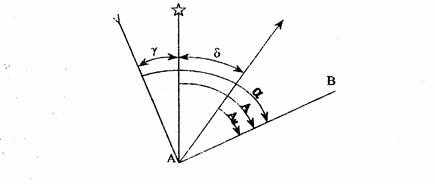
Рис.15 Связь между магнитными азимутами, дирекционными углами и истинными азимутами.

На рис 15 линия со звездочкой есть направление истинного (географического) меридиана, а линия с перевернутой стрелкой показывает расположение осевого меридиана относительно географического. Линия со стрелкой показывает расположение магнитного меридиана относительно географического. В данном случае сближение меридианов западное, а склонение магнитной стрелки восточнее. Имея такой чертеж легко перейти от одного угла ориентирования к другому.

В табл.12 приведены результаты вычисления магнитных азимутов сторон треугольника при γ=-2°20´западное сближение, и δ=4°15´восточное склонение.

Таблица 12. Вычисление магнитных азимутов

Название линий	Дирекционные углы, α	Склонение магнитной стрелки, δ	Сближение меридианов, γ	Магнитный азимут,Ам
АВ	131°15´	+4°15´	-2°20´	124°40´
ВС	262°45´	+4°15´	-2°20´	256°10´
СА	9°15´	+4°15´	-2°20´	2°40´

Вопросы для самоконтроля.

1. Что называется истинным меридианом, параллелью, осевым меридианом?
2. Что означает ориентировать линию?
3. Что называется истинным азимутом, дирекционным углом, магнитным азимутом, румбом линии?
4. Какова зависимость между прямым и обратным азимутом?
5. В чем отличие сближения меридианов в проекции Гаусса-Крюгера от сближения меридианов в общем случае?
6. Что называется склонением магнитной стрелки?
7. Почему ориентирование по магнитному меридиану применяется сравнительно редко?
8. Как вычислить магнитный азимут, если известен географический азимут?
9. Как вычислить магнитный азимут, если известен дирекционный угол?

1. Рельеф и его изображение на картах и планах.

Рельеф местности это совокупность неровностей земной поверхности. Выделяют следующие формы рельефа: гора, котловина, хребет, лощина и седловина. (рис.16). На топографических картах и планах рельеф изображается с помощью горизонталей. Горизонталь это плавная кривая, соединяющая точки с одинаковыми высотами. С геометрической точки зрения горизонталь это след от сечения физической поверхности земли горизонтальной плоскостью. Понятие о горизонтали можно получить, если представить себе местность затопленную до заданной высоты непроточной водой. Береговая линия в этом случае и будет являться горизонталью. Изменяя уровень воды, получим горизонтали с различными высотами. На картах и планах высоты горизонталей изменяют через равные промежутки, которые называют высотой сечения рельефа. Таким образом высота сечения рельефа это расстояние по вертикали между смежными секущими плоскостями (рис.17). Она всегда подписана на топографических картах и планах. При необходимости ее можно определить как разность высот соседних горизонталей. Высоту сечения обозначают h_o. Стандартные высоты сечений рельефа топографических карт равны: 2,5 м(1:10000), 5.0 м (1:25000), 10 м (1:50000), 20 м(1:100000). Топографические планы масштаба 1:500 составляют с высотой сечения 0,25 или 0,5 м; 1:1000– 0.5 или 1,0 м; 1:2000 – 1,0 м.

19. Что такое горизонталь?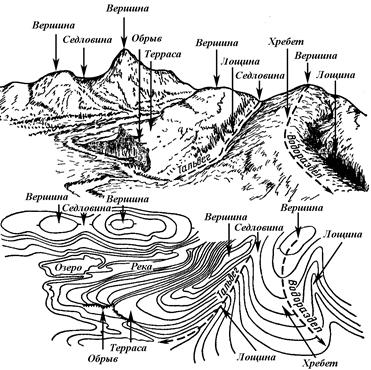

Рис.16. Основные формы рельефа и изображение их горизонталями

Высота сечения зависит от рельефа местности, масштаба и назначения топографического плана. Высота горизонтали всегда кратна высоте сечения рельефа, принятой для составления данной карты (плана). В отдельных случаях, для детализации рельефа, проводят полугоризонтали. Высота сечения в этих случаях равна половине высоты основного сечения рельефа.

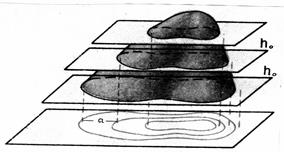
Рис. 17. Сечение рельефа горизонтальными плоскостями

1 Заложение это расстояние вна плане между смежными сплошными горизонталями. По заложению можно судить о крутизне ската. Чем меньше заложение, тем круче скат. Заложение обычно обозначают буквой а (рис.17).

На рис 16 представлены основные формы рельефа: гора; котловина: хребет: лощина и седловина.

Гора, холм - конусообразное возвышение. Наивысшая точка – вершина, боковые поверхности – скаты, линия их слияния с окружающей местностью – подошва.

Котловина (впадина) – замкнутое углубление. Самая низкая ее точка - дно. Боковые поверхности – скаты, а линия их слияния с окружающей местностью – бровка.

Хребет – возвышенность, вытянутая и понижающаяся в одном направлении возвышенность. Скаты хребта при пересечении в верхней части образуют линию, которая называется водораздельной.

Лощина – вытянутое и понижающееся в одном направлении углубление. Скаты лощины при пересечении в нижней части образуют линию, которая называется тальвегом (водосливной линией).

Седловина – место слияния двух хребтов смежных гор. Самая низкая точка седловины называется перевалом. От перевала в обе стороны отходят лощины.

Основной характеристикой рельефа является крутизна ската. О ней можно судить по величине заложения. Чем меньше заложение (расстояние между горизонталями), тем круче скат и наоборот. Для проектирования и строительства зданий и сооруженийК пользуются численными характеристиками крутизны ската, которыми являютсяотносят уклон i или угол наклона линии ν

i_АВ =(H_B-H_A)/d_AB, (314)

а 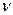= arc tg(H_B-H_A)/d_AB. (154)

Таким образом для определения крутизны ската достаточно определить по карте высоты концов отрезка и его длину. Уклон линии может быть записан или в виде десятичной дроби (i_АВ = 0.0563), или в процентах (i_АВ = 5.63%), или в промиллях (тысячная доля) (i_АВ = 56.3‰).

Из формул (14) и (15) видно, что уклон линии есть значение тангенса угла наклона

i_АВ = tg ν _АВ, а угол наклона ν _АВ = arc tg i_АВ.

При чтении рельефа руководствуются следующими правилами:

1)бергштрихи всегда направлены в сторону понижения;

2)основания цифр, которыми подписаны горизонтали, располагаются в направлении понижения ската;

3) к водоемам и водотокам местность понижается;

4) в одну сторону от горизонтали местность повышается, а в другую понижается;

5) горизонтали перегибаются на водораздельных линиях хребтов и тальвегах лощин;

6) отметка точки, лежащей на горизонтали, равна отметке горизонтали;

7)отметки горизонталей всегда кратны высоте сечения рельефа.

Для отыскания отметки горизонтали находят ближайшую подписанную горизонталь. Отметка искомой будет равна (рис.18).

Н А= Н 0+ nh 0 (16)

где Н 0 – отметка подписанной горизонтали;

n - число горизонталей между подписанной и искомой горизонталью

h0 - высота сечения рельефа.

В формуле знак (+) ставится в случае, если точка А находится выше по склону подписанной горизонтали, а (-) - если ниже. На рис.18 h0=5м, n=2 следовательно НA=210,0м. При отсутствии вблизи определяемой точки подписанной горизонтали, ее отметку находят от ближайшей подписанной отметки характерной точки. В этом случае сначала определяют отметку ближайшей горизонтали. Ее отметка будет кратна высоте сечения рельефа. Например, отметка горизонтали, расположенной ниже вершины горы с Н=216,4 равна 215,0м. От этой горизонтали, руководствуясь описанным выше методом, определяют отметку горизонтали с точкой А.

Рис 18. Определение высоты точки

Если определяемая точка находится между горизонталями, то сначала необходимо определить отметки горизонталей, между которыми они находятся, а затем превышение между горизонталью и определяемой точкой линейным интерполированием

hc=ac h0/a, (17)

где hc - превышение между младшей горизонталью с отметкой Н 0 и точкой С;

a - заложение

ac - расстояние от младшей горизонтали до точки С.

Тогда отметка искомой точки будет равна

Нс=Н0+ hc (18)

Если определяемая точка лежит между горизонталями с одинаковыми отметками: перевал седловины, вершины горы или дно котловины, то отметка в этих случаях принимается равной отметке ближайшей горизонтали плюс (минус) половина высоты сечения рельефа.

Одной из наиболее распространенных задач при проектировании зданий и сооружений на топографических планах является определение крутизны склона, т. е. определение уклона или угла наклона по заданному направлению. Эти характеристики можно измерить или графически (по графикам заложений) или по формулам 14 или 15. Для определения крутизны ската графически необходимо иметь графики заложений.

Задача 6.1.Построить графики заложений для значений ν° и ί, приведенных в таблице 12.

Графики заложений показывают зависимость между крутизной ската и величиной заложения при данной высоте сечения. Так как крутизна ската может быть выражена в градусной мере или процентах, то в соответствии с этими имеется два вида графиков, - для углов наклона и уклонов. Пользоваться такими графиками можно только в случае определения крутизны ската между соседними горизонталями.

Если крутизна ската выражена в градусной мере, то величину заложения a вычисляют по формуле:

a=h0 \ tgν, (19)

а для крутизны ската, выраженной в процентах:

a=h0100/i (20)

где h0 - высота сечения рельефа на карте, выданной для выполнения работы.

Для построения графиков необходимо вычислить заложения a при ν ° и i,

приведенные в таблице 13.

Таблица 13.Исходные данные для построения графиков заложений

Углы наклона	0,5°	1°	2°	3°	4°	5°	7°	10°	20°
Заложения а (м)
Уклоны %
Заложения а (м)

При построении графиков на горизонтальной линии откладывают равные отрезки произвольной длины, в концах которых восстанавливают перпендикуляры, и откладывают на них в масштабе своей карты соответствующее значение из табл.13. Концы перпендикуляров соединяют плавной линией.

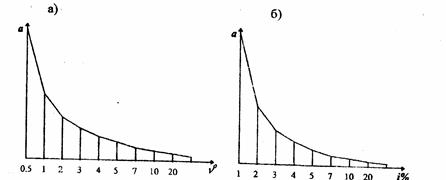
Рис. 19.Графики заложений для уклонов и углов наклон а

---

Дата добавления: 2015-09-01