Читайте также:
|
Эллипсом называют множество точек плоскости, сумма расстояний которых до двух фиксированных точек F1, F2 называемых ФОКУСАМИ есть велечина постоянная равная 2а(а>0)
Каноническое уравнение Эллипса
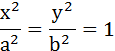
Формула эллипса определяется величеной Ɛ= 
называется эксцентриситет, Ɛ характеризует меру сжатия эллипса.
12.Понятие гиперболы. Её каноническое уравнение. Асимптоты. Построение гиперболы. Эксцентриситет.
Гиперболой называется множество точек плоскости модуль разности расстояний которых до двух фиксированных точек F1,F2 - фокуоы, есть величена постоянная равная 2а(а>0)
Каноническое уравнение гиперболы
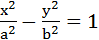
Асимптота - это прямые к которым неограничено близко приблежаются точки гиперболы, при удалении в бесконечность от начала кординат
Ɛ= 
характеризуют меру сжатия гиперболы к оси ОХ
13. Понятие параболы. Построение параболы по её каноническому уравнению (4 случая).
Пораболой называется множество точек плоскости равноудалённых от точки F называемой фокусом и прямой d называемой директриссой
Каноническое уравнение параболы
при построении параболы рекомендуется получить из уравнение параболы одну, две точки для того чтобы определить размер ветвей
Дата добавления: 2015-09-02; просмотров: 89 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Смешанное произведение в координатной форме(вывод) | | | Понятие цилиндрической поверхности. Эллиптический, гиперболический, параболический цилиндры, пары пересекающихся или параллельных плоскостей. |