
Читайте также:
|
Определение. Корнем n -ой степени из комплексного числа называется такое комплексное число, n -я степень которого равна подкоренному числу.
Из этого определения следует, что из равенства  следует равенство
следует равенство  .
.
 Из равенства комплексных чисел следует
Из равенства комплексных чисел следует 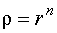 , а аргументы отличаются на число, кратное
, а аргументы отличаются на число, кратное  ;
; 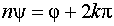 . Отсюда
. Отсюда 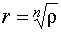 ,
,  . Здесь
. Здесь 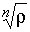 есть арифметическое значение корня, а k – любое целое число. Таким образом, получается формула
есть арифметическое значение корня, а k – любое целое число. Таким образом, получается формула
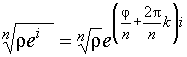 .
.
В этой формуле число k может принимать всевозможные целые значения, но различных значений корня будет только n и они соответствуют значениям k = 0, 1, 2, …, n - 1.
Докажем этот факт. Действительно, правые части в этой формуле различны тогда, когда аргументы 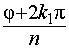 и
и 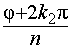 отличаются на величину, не кратную
отличаются на величину, не кратную  , и будут одинаковыми, если указанные аргументы отличаются на величину, кратную
, и будут одинаковыми, если указанные аргументы отличаются на величину, кратную  . Поэтому разность
. Поэтому разность
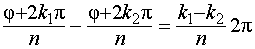
не может быть кратна  . Из этого результата и следует, что любым подряд взятым n целым числам k соответствуют n различных значений корня.
. Из этого результата и следует, что любым подряд взятым n целым числам k соответствуют n различных значений корня.
Пусть теперь k 3– целое число, не входящее в эту последовательность подряд взятых значений k. Это число можно представить в виде k 3= gn + ki, где g – целое число, а ki – одно из чисел этого ряда, поэтому  , то есть значению k 3 соответствует то же значение корня, что и значению ki.
, то есть значению k 3 соответствует то же значение корня, что и значению ki.
Вывод: корень n -ой степени из комплексного числа имеет n различных значений. Исключением из этого правила является лишь частный случай, когда извлекается корень из нуля. В этом случае все значения корня равны нулю.
Дата добавления: 2015-08-27; просмотров: 34 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Модуль частного равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя. | | | Глава 4.3 Векторная алгебра |