Теорема. Полный дифференциал функции двух независимых переменных равен сумме произведений частных производных функции на дифференциалы соответствующих независимых переменных.
И мы доказали формулу 6. | ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ | ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ | Непрерывные функции обладают следующими свойствами. | Теорема 3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль. | Классификация точек разрыва | ПРОИЗВОДНАЯ ФУНКЦИИ | Геометрический смысл производной | Геометрический смысл дифференциала функции | Дифференцируемость функции нескольких переменных. |
dZ=f'x(x,y)dx+f'y(x,y)dy или 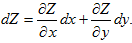
Так как  dx=dxZ и
dx=dxZ и  dy=dyZ, то dZ=dxZ+dyZ, т.е. дифференциал функции двух независимых переменных равен сумме ее частных дифференциалов.
dy=dyZ, то dZ=dxZ+dyZ, т.е. дифференциал функции двух независимых переменных равен сумме ее частных дифференциалов.
Определение дифференциала переносится на функции любого числа независимых переменных.
Пример 7.  Найти dz
Найти dz
Дата добавления: 2015-08-27; просмотров: 52 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.006 сек.)

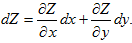
 dx=dxZ и
dx=dxZ и  dy=dyZ, то dZ=dxZ+dyZ, т.е. дифференциал функции двух независимых переменных равен сумме ее частных дифференциалов.
dy=dyZ, то dZ=dxZ+dyZ, т.е. дифференциал функции двух независимых переменных равен сумме ее частных дифференциалов. Найти dz
Найти dz