Читайте также:
|
В частном случае, при 
, получаем эквивалентность
) 
.
7) 
(
). Для доказательства сделаем замену 
и выразим 
через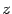 
: 
. Согласно формуле 6, 
при 
, откуда 
. Из непрерывности логарифма следует, что 
и, значит,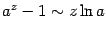 
при 
. В этой формуле осталось лишь сменить обозначение переменного 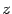на , чтобы получить формулу 7.
В частном случае, при , получаем эквивалентность
) 
.
Сведём теперь полученные формулы в итоговую таблицу. Всюду в ней .
| 1) |  .
|
| 2) |  .
|
| 3) |  .
|
| 4) |  .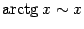
|
| 5) |  .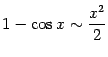
|
| 6) |  ().
|
| )
| .
|
| 7) | ().
|
| )
| .
|
Приведём примеры применения табличных формул для раскрытия неопределённостей вида 
.
Дата добавления: 2015-08-27; просмотров: 41 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Где степень p - действительное число. | | | ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ |