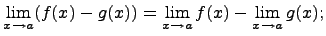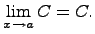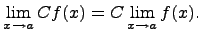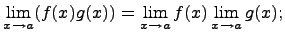Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Предел разности равен разности пределов, если каждый из них существует, т.е.

Предел функции нескольких переменных | Непрерывность функции многих переменных | Свойства непрерывных функций | Классификация элементарных функций. | Множество значений функции. | Числовые последовательности | Свойства числовых последовательностей | Предел последовательности | Случай, когда последовательность не имеет предела. | Предел функции |


Читайте также:
  1. A) для передачи и распределения энергии
  2. C) для протекания разности токов фаз (полюсов) при неравномерной их нагрузке
  3. I Сущность права . Определение его понятия .
  4. I. Определение фокусного расстояния собирающей линзы
  5. I. ПРЕДЕЛЫ
  6. I. ПРЕДЕЛЫ
  7. II. Дать определение анатомическим терминам.

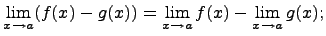
  1. Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

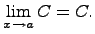
  1. Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

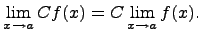
  1. Предел произведения Предел произведения равен произведению пределов, если каждый из них существует, т.е.

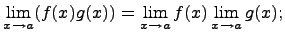
  1. Предел частного

Дата добавления: 2015-08-27; просмотров: 56 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Теорема 4 (свойства бесконечно малых функций).| Где степень p - действительное число.
mybiblioteka.su - 2015-2025 год. (0.008 сек.)