
|
Читайте также: |
Рассмотрим некоторые случаи изменения функции при стремлении аргумента х к некоторому пределу а или к бесконечности.
Определение 1. Пусть функция  определена в некоторой окрестности точки а или в некоторых точках этой окрестности. Функция
определена в некоторой окрестности точки а или в некоторых точках этой окрестности. Функция 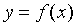 стремится к пределу
стремится к пределу  при х, стремящемся к
при х, стремящемся к  , если для каждого положительного числа
, если для каждого положительного числа  , как бы мало оно ни было, можно указать такое положительное число
, как бы мало оно ни было, можно указать такое положительное число  , что для всех х, отличных от
, что для всех х, отличных от 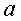 и удовлетворяющих неравенству
и удовлетворяющих неравенству  , имеет место неравенство
, имеет место неравенство
 .
.
Если  есть предел функции f(x) при
есть предел функции f(x) при  , то пишут:
, то пишут:  или f (x)
или f (x) 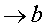 при
при 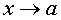 .
.
Если 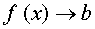 при
при  , то на графике функции
, то на графике функции  , т.к. из неравенства
, т.к. из неравенства  следует неравенство
следует неравенство 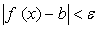 , то это значит, что для всех точек х, отстоящих от точки
, то это значит, что для всех точек х, отстоящих от точки 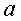 не далее чем на
не далее чем на  , точки М графика функции
, точки М графика функции  лежат внутри полосы шириной
лежат внутри полосы шириной  , ограниченной прямыми
, ограниченной прямыми 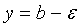 и
и  (рис. 2).
(рис. 2).
 Рис. 2
Рис. 2
Рассмотрим переменную величину у = f (х). При этом считать, как и всюду в дальнейшем, что из двух значений функции последующим является то значение, которое соответствует последующему значению аргумента. Если определенная так переменная величина у при  стремится к некоторому пределу
стремится к некоторому пределу 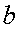 , то будем писать
, то будем писать

и говорить, что функция у = f (х) стремится к пределу b при  .
.
Легко доказать, что оба определения предела функции эквивалентны. Замечание.
Если f ( x ) стремится к пределу b 1 при х, стремящемся к некоторому числу 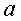 так, что x принимает только значения, меньшие
так, что x принимает только значения, меньшие 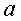 , то пишут
, то пишут  и называют b 1 пределом функции f ( x ) в точке
и называют b 1 пределом функции f ( x ) в точке 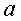 слева. Если х принимает только значения большие, чем
слева. Если х принимает только значения большие, чем 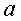 , то пишут
, то пишут  и называют b 2, пределом функции в точке
и называют b 2, пределом функции в точке 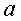 справа.
справа.
Можно доказать, что если, предел справа и предел слева существуют и равны, т. е.  , то b и будет пределом в смысле данного выше определения предела в точке
, то b и будет пределом в смысле данного выше определения предела в точке 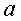 . И обратно, еслт предел функции b в точке
. И обратно, еслт предел функции b в точке 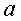 , то существуют пределы функции в точке
, то существуют пределы функции в точке 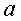 справа и слева и они равны.
справа и слева и они равны.
Замечание.
Для существования предела функции при  не требуется, чтобы функция была определена в точке
не требуется, чтобы функция была определена в точке 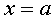 . При нахождении предела рассматриваются значения функции в окрестности точки
. При нахождении предела рассматриваются значения функции в окрестности точки 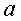 , отличные от
, отличные от 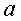 ; это положение наглядно иллюстрируется следующим примером.
; это положение наглядно иллюстрируется следующим примером.
Пример. Докажем, что  . Здесь функция
. Здесь функция  не определена при х = 2.
не определена при х = 2.
Нужно доказать, что при произвольном  найдется такое
найдется такое  , что будет выполняться неравенство
, что будет выполняться неравенство
 , (1)
, (1)
если | х — 2 | <  . Но при х
. Но при х  2 неравенство (1) эквивалентно неравенству
2 неравенство (1) эквивалентно неравенству
 (2)
(2)
или  .
.
Таким образом, при произвольном  неравенство (1) будет выполняться, если будет выполняться неравенство (2) (здесь
неравенство (1) будет выполняться, если будет выполняться неравенство (2) (здесь  ). А это и значит, что данная функция при
). А это и значит, что данная функция при  имеет пределом число 4.
имеет пределом число 4.
Рассмотрим некоторые случаи изменения функции при 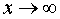 . Определение 2. Функция f(x) стремится к пределу
. Определение 2. Функция f(x) стремится к пределу 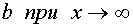 , если для каждого произвольно малого положительного числа
, если для каждого произвольно малого положительного числа  можно указать такое положительное число N, что для всех значении х, удовлетворяющих неравенству
можно указать такое положительное число N, что для всех значении х, удовлетворяющих неравенству 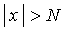 , будет выполняться неравенство
, будет выполняться неравенство  .
.
 Зная смысл символов:
Зная смысл символов:  очевидным является и смысл выражений:
очевидным является и смысл выражений:
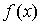 стремится к b при
стремится к b при  и
и
 стремится к b при
стремится к b при 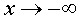 ,
,
которые символически записываются так:
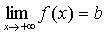 ,
, 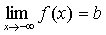
30)(бесконечно большая функция). Функция называется бесконечно большой при x ® a или в точке a, если для любого положительного числа e найдется такое положительное d(e), что для всех x№ a и удовлетворяющих условию |x-a|<d будет выполнено неравенство |f(x)|>e.
Аналогично можно дать определение бесконечно большой при x® Ґ. Приведем его в символической записи:
lim x ® Ґ f (x) = Ґ Ы " e>0 $ d(e)>0 " x:|x|> d |f (x) |> e.
Предложение 1. a(x) бесконечно малая функция при x ® a Ы 1 / a(x) — бесконечно большая при x ® a
Пример 11. y = x2 – бесконечно малая функция при x ® 0, а y = 1/x2 – бесконечно большая при x ® 0.
1. Сумма бесконечно больших величин есть величина бесконечно большая:
 . (4.20)
. (4.20)
2. Произведение бесконечно больших величин есть величина бесконечно большая:
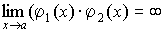 . (4.21)
. (4.21)
3. Произведение бесконечно большой величины на константу С, или на функцию, имеющую конечный предел  , есть величина бесконечно большая:
, есть величина бесконечно большая:
 (4.22)
(4.22)
Связь бесконечно малой и бесконечно большой величины
Величина, обратная бесконечно малой величине, есть величина бесконечно большая, и наоборот, величина, обратная бесконечно большой величине, есть величина бесконечно малая.
Пусть 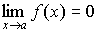 и
и 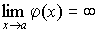 , тогда
, тогда 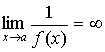 и
и  .
.
Символически можно записать:
 и
и 
Примеры:
1)  ;
;
2) 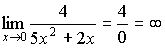 ;
;
3) 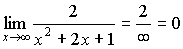 .
.
31) (бесконечно малая функция). Функция называется бесконечно малой в точке a или при x ® a, если
lim x ® af (x) = 0
Пример 10.
f (x) = 1 /x, x ® ¥
f (x) = x 2, x ® 0
f (x) = 1-cos x, x ® 0
Заметим, что если функция f(x) имеет предел в точке a, равный A, то функция a(x) = f(x)-A является бесконечно малой в точке a. То есть, если функция f(x) имеет предел A в точке a, то f(x) = A+a, где limx® aa (x) = 0.
Отметим некоторые свойства бесконечно малых функций.
Дата добавления: 2015-08-27; просмотров: 76 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Случай, когда последовательность не имеет предела. | | | Теорема 4 (свойства бесконечно малых функций). |