Обратные тригонометрические функции, их свойства и графики.

Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки "арк" обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.

Функция арксинус y = arcsin(x).

Изобразим график функции арксинус:

Свойства функции арксинус y = arcsin(x).

• Областью определения функции арксинус является интервал отминус единицы до единицы включительно: .
• Область значений функции y = arcsin(x): .
• Функция арксинус - нечетная, так как .
• Функция y = arcsin(x) возрастает на всей области определения, то есть, при .
• Функция вогнутая при , выпуклая при .
• Точка перегиба (0; 0), она же ноль функции.
• Асимптот нет.

Функция арккосинус y = arccos(x).

График функции арккосинус имеет вид:

Свойства функции арккосинус y = arccos(x).

• Область определения функции арккосинус: .
• Область значений функции y = arccos(x): .
• Функция не является ни четной ни нечетной, то есть, она общего вида.
• Функция арккосинус убывает на всей области определения, то есть, при .
• Функция вогнутая при , выпуклая при .
• Точка перегиба .
• Асимптот нет.

Функция арктангенс y = arctg(x).

График функции арктангенс имеет вид:

Свойства функции арктангенс y = arctg(x).

• Область определения функции y = arctg(x): .
• Область значений функции арктангенс: .
• Функция арктангенс - нечетная, так как .
• Функция возрастает на всей области определения, то есть, при .
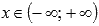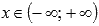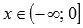• Функция арктангенс вогнутая при , выпуклая при .
• Точка перегиба (0; 0), она же ноль функции.
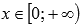• Горизонтальными асимптотами являются прямые при и при . На чертеже они показаны зеленым цветом.

Функция арккотангенс y = arcctg(x).

Изобразим график функции арккотангенс:

Свойства функции арккотангенс y = arcctg(x).

• Областью определения функции арккотангенс является все множество действительных чисел: .
• Область значений функции y = arcctg(x): .
• Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
• Функция убывает на всей области определения, то есть, при .
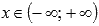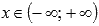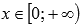• Функция вогнутая при , выпуклая при .
• Точка перегиба .
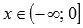• Горизонтальными асимптотами являются прямые при (на чертеже показана зеленым цветом) и y = 0 при .

23)Пространство Rⁿ

Определение. Множество упорядоченных наборов действительных чисел M (x ₁, x ₂, …, x_n), для которых определено расстояние

,

называется пространством Rⁿ. Элементы M (x ₁, x ₂, …, x_n) называются точками пространства R ⁿ.
Определение. ε – окрестностью точки M₀(x ₁₀, x ₂₀, …, x_{n 0}) Rⁿ называется множество точек M (x ₁, x ₂, …, x_n) Rⁿ таких, что расстояние их до точки М₀ меньше ε:

.

(смотри рисунок.)
Определение. Точка М₀ = (a ₁, a ₂, …, a_n) называется точкой сгущения множества V Rⁿ, если в любой как угодно малой окрестности О _ε(М₀) найдётся хотя бы одна точка М V и М ≠ М₀, такая, что М О_ε(М₀).
Определение. Пусть M₀ (x ₁₀, x ₂₀, …, x _n0) Rⁿ, δ _i > 0, i = 1, 2, …, n. Множество

называется n – мерным параллелепипедом, а точка М₀ — его центром. Если δ₁ = δ₂ = … = δ _n = δ, то P (x, δ, δ, δ, …, δ) называется n – мерным кубом с центром в точке М₀ и обозначается Р (М₀, δ).
Определение. Всякий n – мерный параллелепипед P (M₀, δ₁, δ₂, …, δ _n) называется прямоугольной окрестностью точки М₀.
Лемма. Какова бы ни была ε – окрестность О(М₀, ε) точки М₀ Rⁿ существует её прямоугольная окрестность P(M₀, δ₁, δ₂, …, δ _n),такая, что P(M₀, δ₁, δ₂, …, δ _n) О(М₀, ε), и наоборот, какова бы ни была прямоугольная окрестность P(M₀, δ₁, δ₂, …, δ _n) точки М₀ Rⁿ, существует её ε – окрестность О (М₀, ε), такая, что О (М₀, ε) P (M₀, δ₁, δ₂, …, δ _n).
Доказательство леммы опирается на неравенства

.

Если М О (М₀, ε), то d (M, M₀) < ε, и в силу неравенства

следуют неравенства | x_i - x_{i 0} | < ε для всех i = 1, 2, …, n. Это означает, что М P (M₀, ε).
Обратно, пусть М P (M₀, δ₁, δ₂, …, δ_n). Тогда в силу неравенства

имеем

а это означает, что М О (М₀, ε). Что и требовалось доказать.

Дата добавления: 2015-08-27