
Читайте также:
|
Векторное произведение векторов
1. Векторы 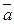 и
и 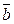 взаимно перпендикулярны. Зная, что
взаимно перпендикулярны. Зная, что  , вычислить:
, вычислить:
1.1. 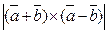 . 1.2.
. 1.2.  .
.
2. Даны координаты  и
и  . Найти координаты векторных произведений:
. Найти координаты векторных произведений:
2.1.  . 2.2.
. 2.2.  . 2.3.
. 2.3.  .
.
3. Сила  приложена к точке
приложена к точке 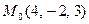 . Определить момент этой силы относительно точки
. Определить момент этой силы относительно точки  , величину и направляющие косинусы момента.
, величину и направляющие косинусы момента.
4. Вычислить синус угла, образованного векторами 
и  .
.
5. Даны точки  ,
,  и
и  . Вычислить площадь треугольника
. Вычислить площадь треугольника 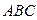 .
.
6. Даны вершины треугольника  ,
,  и
и  . Вычислить длину его высоты, опущенной из вершины
. Вычислить длину его высоты, опущенной из вершины  на сторону
на сторону 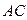 .
.
7. Вектор  , перпендикулярный к оси Oz и к вектору
, перпендикулярный к оси Oz и к вектору  , образует острый угол с осью Ox. Зная, что
, образует острый угол с осью Ox. Зная, что  , найти его координаты.
, найти его координаты.
Смешанное произведение векторов
8. Доказать, что четыре точки  ,
,  ,
,  ,
,  лежат в одной плоскости.
лежат в одной плоскости.
9. Установить, компланарны ли векторы  если:
если:
9.1. 
9.2. 
9.3. 
10. Даны вершины треугольной пирамиды: 


 . Найти объем пирамиды и длину его высоты, опущенной из вершины
. Найти объем пирамиды и длину его высоты, опущенной из вершины  .
.
11. Объем треугольной пирамиды  три его вершины находятся в точках
три его вершины находятся в точках 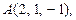
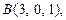
 Найти координаты четвертой вершины
Найти координаты четвертой вершины  , если известно, что она лежит на оси Oy.
, если известно, что она лежит на оси Oy.
12. Какую тройку векторов (правую, левую) образуют векторы:  ?
?
13. Образуют ли базис векторы  ?
?
Дополнительные задания
Д-1. Найти пр. 

Д-2. Найти орт вектора  , где
, где  ,
, 
Д-3. Найти площадь параллелограмма  , если его тремя последовательными вершинами являются точки
, если его тремя последовательными вершинами являются точки 
Д-4. Векторы  и
и  являются сторонами параллелограмма. Найти площадь параллелограмма, построенного на его диагоналях.
являются сторонами параллелограмма. Найти площадь параллелограмма, построенного на его диагоналях.
Д-5. Найти длину опущенной на сторону 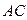 высоты треугольника, если
высоты треугольника, если 
Д-6. Найти значение 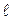 , при котором четыре точки
, при котором четыре точки  и
и  лежат в одной плоскости.
лежат в одной плоскости.
Д-7. При каких значениях 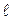 тройка векторов
тройка векторов 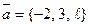 ,
, 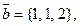
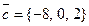 будет левой и объем параллелепипеда, на них построенного, равен 5 ед3?
будет левой и объем параллелепипеда, на них построенного, равен 5 ед3?
Д-8. При каком значении 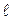
 если
если 
 ?
?
Д-9. Найти значение 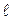 , при котором
, при котором 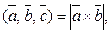 если
если 

Д-10. Найти значение 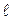 , при котором
, при котором  если
если 

Д-11. На векторах 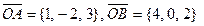 и
и  построен параллелепипед. Найти длину его высоты, опущенной из вершины
построен параллелепипед. Найти длину его высоты, опущенной из вершины 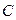
на грань векторов 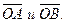
Д-12. Объем треугольной пирамиды  равен 12. Найти координаты вершины
равен 12. Найти координаты вершины  , если
, если  а точка
а точка  лежит на оси Oz, причем векторы
лежит на оси Oz, причем векторы 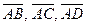 образуют левую тройку.
образуют левую тройку.
Д-13. Вектор 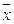 , перпендикулярный векторам
, перпендикулярный векторам  и
и  , образует с осью Oy тупой угол. Зная, что
, образует с осью Oy тупой угол. Зная, что  найти его координаты.
найти его координаты.
Д-14. Найти единичный вектор, перпендикулярный векторам  и
и 
Д-15. Векторы  имеют равные длины и образуют попарно равные углы. Найти вектор
имеют равные длины и образуют попарно равные углы. Найти вектор  , если
, если 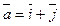 ,
, 
Д-16. Доказать, что при любых векторах  векторы
векторы 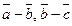
и  компланарны.
компланарны.
Д-17. Показать, что векторы  и
и 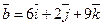 могут быть взяты за ребра куба. Найти третье ребро куба.
могут быть взяты за ребра куба. Найти третье ребро куба.
Д-18. Векторы 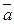 и
и 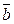 образуют угол 45о. Найти площадь треугольника, построенного на векторах
образуют угол 45о. Найти площадь треугольника, построенного на векторах 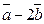 и
и  если
если 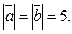
Д-19. Дана пирамида с вершинами в точках 
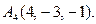 Найти:
Найти:
Д-19.1. Длины ребер  Д-19.2. Площадь грани
Д-19.2. Площадь грани  Д-19.3. Угол между ребрами
Д-19.3. Угол между ребрами  и
и  Д-19.4. Объем пирамиды.
Д-19.4. Объем пирамиды.
Д-19.5. Длину высоты, опущенной на грань 
Итоговый самоконтроль
С-1. Как построить вектор, перпендикулярный двум векторам
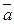 и
и 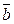 ?
?
С-2. Чему равна проекция 
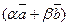 ?
?
С-3. Векторы  ,
,  Какому условию удовлетворяют векторы
Какому условию удовлетворяют векторы  и
и  ?
?
С-4. Как установить компланарность трех векторов, заданных своими координатами?
С-5. Как установить коллинеарность двух векторов, заданных своими координатами?
С-6. Как установить, образуют ли базис в R 3 три вектора, заданные своими координатами?
С-7. Доказать, что векторы 
 и
и  компланарны тогда и только тогда, когда среди чисел
компланарны тогда и только тогда, когда среди чисел 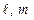 и
и  есть равные.
есть равные.
С-8. Пусть  — некомпланарные векторы. Как связаны
— некомпланарные векторы. Как связаны
между собой числа  если векторы
если векторы 
 и
и  компланарны?
компланарны?
С-9. Векторы  удовлетворяют условию
удовлетворяют условию  Доказать, что векторы
Доказать, что векторы  компланарны.
компланарны.
С-10. Доказать, что если векторы  удовлетворяют равенству
удовлетворяют равенству  то
то 
С-11. Даны единичные векторы  Зная, что
Зная, что  , доказать равенство
, доказать равенство 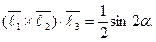
С-12. Зная, что  , найти соотношение между векторами
, найти соотношение между векторами  не содержащее коэффициентов
не содержащее коэффициентов  и
и 
С-13. Чему равно смешанное произведение векторов  и
и  , где
, где  и
и  — произвольные числа?
— произвольные числа?
С-14. Чему равно:
1. 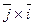 . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
С-15. Какому условию должны удовлетворять векторы 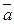 и
и 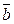 , чтобы векторы
, чтобы векторы  и
и  были коллинеарны?
были коллинеарны?
С-16. При каких значениях 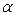 и
и  векторы
векторы  и
и  коллинеарны?
коллинеарны?
С-17. Чему равно векторное произведение противоположных векторов?
С-18. Изменится ли векторное произведение, если к одному из сомножителей прибавить вектор, коллинеарный другому сомножителю?
С-19. Верны ли утверждения:
а) 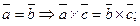 б)
б) 
в)  г)
г)  .
.
Ответы поясните.
С-20. Доказать, что 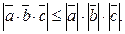
Дата добавления: 2015-08-27; просмотров: 224 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Векторное и смешанное произведения векторов, их вычисление, свойства и применения | | | Уравнения плоскости в . Взаимное расположение плоскостей |