
Читайте также:
|
1. Найти собственные значения и собственные векторы матрицы:
1.1.  . 1.2.
. 1.2.  .
.
1.3.  . 1.4.
. 1.4. 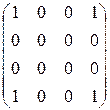 .
.
1.5.  . 1.6.
. 1.6.  .
.
1.7.  . 1.8.
. 1.8.  .
.
1.9.  . 1.10. А =
. 1.10. А = 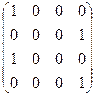
Дополнительные задания
Д-1. Определить собственные значения и собственные векторы матрицы:
Д-1.1. 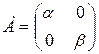 . Д-1.2.
. Д-1.2.  .
.
Д-2. Доказать, что собственные значения диагональной матрицы равны ее диагональным элементам.
Д-3. Все собственные значения матрицы  равны
равны  . Найти все собственные значения матриц:
. Найти все собственные значения матриц:
а) 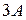 ; б)
; б)  .
.
Д-4. Найти характеристические числа и собственные векторы матриц:
Д-4.1.  . Д-4.2.
. Д-4.2.  .
.
Д-4.3.  . Д-4.4.
. Д-4.4.  .
.
Д-4.5. 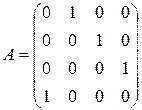 . Д-4.6.
. Д-4.6.  .
.
Д-5. Найти все векторы  , удовлетворяющие уравнению
, удовлетворяющие уравнению  , если матрица
, если матрица  имеет вид:
имеет вид:
Д-5.1.  . Д-5.2.
. Д-5.2.  .
.
Д-5.3. 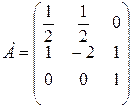 .
.
Д-6. Найти решения СЛУ при любых значениях параметра l:
Д-6.1.  . Д-6.2.
. Д-6.2.  .
.
Итоговый самоконтроль
С-1. Чему равны собственные значения треугольной матрицы?
С-2. Имеет ли собственные значения вырожденная матрица?
С-3. Что можно сказать о собственных значениях матрицы  , если известны собственные значения матрицы
, если известны собственные значения матрицы  ?
?
С-4. Верно ли утверждение о том, что все n -мерные векторы — являются собственными векторами матрицы  ?
?
С-5. Что можно сказать о корнях характеристического уравнения  , если матрица
, если матрица  симметрическая?
симметрическая?
С-6. Если  — собственные значения матрицы
— собственные значения матрицы  , то чему равны собственные значения матриц
, то чему равны собственные значения матриц 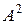 ,
,  ?
?
Дата добавления: 2015-08-27; просмотров: 86 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение систем линейных уравнений методом Гаусса. | | | Линейные операции над векторами. Линейная зависимость и независимость системы векторов. Базис |