
Читайте также:
|
1. Вычислить определители 2-го порядка:
1.1.  . 1.2.
. 1.2.  . 1.3.
. 1.3.  .
.
1.4. 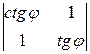 . 1.5.
. 1.5.  .
.
2. Вычислить определители 3-го порядка по правилу Саррюса и разложением по элементам строки или столбца:
2.1.  . 2.2.
. 2.2.  . 2.3.
. 2.3.  .
.
2.4.  . 2.5.
. 2.5.  .
.
3. Вычислить определители, используя их свойства:
3.1.  . 3.2.
. 3.2. 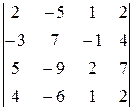 .
.
3.3. 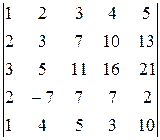 . 3.4.
. 3.4.  .
.
4. Решить уравнения:
4.1.  . 4.2.
. 4.2. 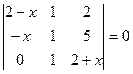 . 4.3.
. 4.3.  .
.
5. Решить неравенства:
5.1.  . 5.2.
. 5.2.  .
.
6. Решить СЛУ по формулам Крамера:
6.1.  . 6.2.
. 6.2. 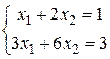 .
.
6.3.  . 6.4.
. 6.4. 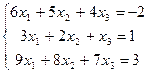 .
.
6.5.  . 6.6.
. 6.6. 
7. При каких значениях параметров система имеет единственное решение?
7.1.  . 7.2.
. 7.2.  . 7.3.
. 7.3.  .
.
8. При каких значениях параметров система несовместна?
8.1. 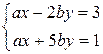 . 8.2.
. 8.2.  . 8.3.
. 8.3. 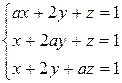 .
.
Дополнительные задания
Д-1. Вычислить определители:
Д-1.1.  . Д-1.2.
. Д-1.2.  . Д-1.3.
. Д-1.3.  .
.
Д-1.4.  . Д-1.5.
. Д-1.5.  . Д-1.6.
. Д-1.6.  .
.
Д-1.7. 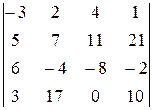 . Д-1.8.
. Д-1.8.  .
.
Д-1.9.  .
.
Д-2. Решить уравнения:
Д-2.1.  . Д-2.2.
. Д-2.2. 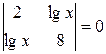 . Д-2.3.
. Д-2.3.  .
.
Д-2.4.  . Д-2.5.
. Д-2.5.  .
.
Д-3. Доказать равенство:
Д-3.1.  .
.
Д-3.2. 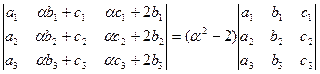 .
.
Д-4. Найти решение СЛУ, используя формулы Крамера:
Д-4.1.  . Д-4.2.
. Д-4.2.  .
.
Д-5. Найти коэффициенты многочлена  , удовлетворяющие условиям
, удовлетворяющие условиям  ,
,  ,
, 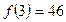 .
.
Итоговый самоконтроль
С-1. Чему равен определитель треугольной матрицы?
С-2. Что известно о произведении определителей матриц и определителе их произведения?
С-3. Можно ли утверждать, что определитель суммы матриц равен сумме их определителей? Если да, приведите примеры.
С-4. Что можно сказать об определителях матрицы 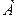 и транспонированной матрицы
и транспонированной матрицы  ?
?
С-5. Что произойдет с определителем, все элементы какой-либо строки (столбца) которого умножат на одно и то же число l:
а) отличное от нуля? б) равное нулю?
С-6. Не вычисляя определителя 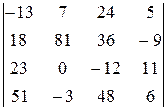 , доказать, что он делится нацело на числа 2, 3, 4, 6. Делится ли он еще на какие-нибудь числа?
, доказать, что он делится нацело на числа 2, 3, 4, 6. Делится ли он еще на какие-нибудь числа?
С-7. Могут ли быть равными определители разных порядков? Ответ поясните.
С-8. Докажите равенство определителей
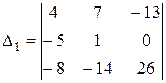 и
и  ,
,
не вычисляя их.
С-9. Может ли определитель 2-го порядка быть больше определителя 3-го порядка?
С-10. Как изменится определитель, если к каждой строке, кроме первой, прибавить первую строку?
С-11. Как изменится определитель, если ко всем строкам (в т. ч. и к первой) прибавить первую строку?
С-12. Как изменится определитель, если его первый столбец разделить на 2?
С-13. Как изменится определитель, если первую строку умножить на 2 и прибавить к ней вторую строку?
С-14. Как изменится определитель, если из каждого столбца, кроме последнего, вычесть последний столбец?
С-15. Изменится ли определитель, если из каждого столбца, в т. ч. и из последнего, вычесть последний столбец?
С-16. Изменится ли определитель, если один из равных столбцов заменить столбцом из нулей?
С-17. Могут ли различные методы решения линейных систем дать различные ответы?
С-18. Изменится ли решение системы, если два уравнения поменять местами?
Дата добавления: 2015-08-27; просмотров: 100 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Раздел 4. Координатный метод. Прямая и плоскость. | | | Линейные операции над матрицами. Умножение матриц. Обратная матрица |