
Читайте также:
|
1. Найти ранг матицы методом элементарных преобразований:
1.1.  1.2.
1.2. 
1.3.  1.4.
1.4. 
1.5.  1.6.
1.6. 
2. Найти ранг матрицы методом окаймляющих миноров и указать один из базисных миноров:
2.1. 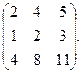 2.2.
2.2.  2.3.
2.3. 
3. Исследовать СЛУ и, если она совместна, найти решение методом
Гаусса:
3.1.  . 3.2.
. 3.2. 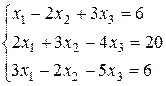 .
.
3.3.  . 3.4.
. 3.4.  .
.
3.5. 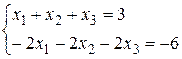 . 3.6.
. 3.6.  .
.
3.7. 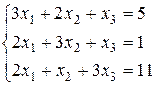 . 3.8.
. 3.8. 

3.9.  3.10.
3.10. 
Дополнительные задания
Д-1. Найти ранг матрицы:
Д-1.1.  Д-1.2.
Д-1.2. 
Д-1.3. 
Д-2. Найти ранг матрицы, содержащей параметр a:
Д-2.1.  Д-2.2.
Д-2.2.  Д-2.3.
Д-2.3. 
Д-3. Решить СЛУ методом Гаусса:
Д-3.1.  . Д-3.2.
. Д-3.2.  .
.
Д-3.3.  . Д-3.4.
. Д-3.4. 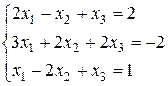 .
.
Д-3.5.  . Д-3.6.
. Д-3.6. 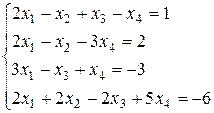 .
.
Д-3.7.  . Д-3.8.
. Д-3.8.  .
.
Д-4. Найти решение СЛУ, содержащей параметры:
Д-4.1.  . Д-4.2.
. Д-4.2.  .
.
Д-4.3.  . Д-4.4.
. Д-4.4. 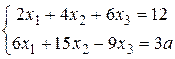 .
.
Д-5. Известно, что СЛУ совместна. Какому числу равен ранг расширенной системы?
Д-5.1. 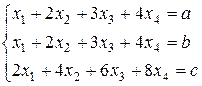 . Д-5.2.
. Д-5.2.  .
.
Д-5.3. 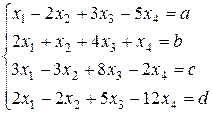 . Д-5.4.
. Д-5.4.  .
.
Д-6. Решить СЛУ методом Гаусса:
Д-6.1.  . Д-6.2.
. Д-6.2.  .
.
Д-6.3. 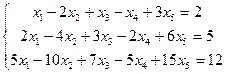 Д-6.4.
Д-6.4. 
Итоговый самоконтроль
С-1. Изменится ли ранг матрицы при ее транспонировании?
С-2. Может ли ранг матрицы быть:
а) меньше нуля;
б) равным нулю;
в) равным 2,5;
г) больше числа строк матрицы;
д) меньше числа столбцов.
С-3. Изменится ли ранг матрицы при добавлении к ней строки, элементы которой пропорциональны элементам любой из имеющихся строк?
С-4. Как отличаются ранги матриц 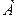 и
и  ?
?
С-5. Чему равен ранг матрицы, все строки которой пропорцио-
нальны?
С-6. Может ли СЛУ иметь три решения? Одно решение?
С-7. Могут ли быть эквивалентными СЛУ, главные матрицы которых имеют равное число столбцов, но разное число строк?
С-8. Изменится ли решение системы, если к ней приписать уравнение?
С-9. Изменится ли решение несовместной системы, если к ней приписать уравнение?
С-10. Если совокупность  — решение однородной системы, можно ли утверждать, что совокупность
— решение однородной системы, можно ли утверждать, что совокупность  также является решением системы?
также является решением системы?
С-11. Докажите, что если  — ненулевое решение однородной системы и
— ненулевое решение однородной системы и  произвольное число, то и
произвольное число, то и  также является решением этой системы.
также является решением этой системы.
С-12. Что можно сказать о рангах матриц СЛУ, если они имеют одинаковое общее решение?
С-13. Что можно сказать о СЛУ, если  ,
, 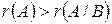 ?
?
Дата добавления: 2015-08-27; просмотров: 100 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение систем линейных уравнений матричным способом. Решение матричных уравнений | | | Собственные векторы и собственные значения матрицы |