Читайте также:
|
1. Лежит ли точка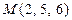 
на плоскости 
?
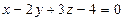2. Построить плоскость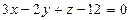 
.
3. Найти объем пирамиды, ограниченной координатными плоскостями и плоскостью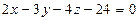 
.
4. Составить уравнение плоскости, проходящей через точку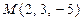 
и имеющей нормальный вектор 
.
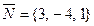5. Составить уравнение плоскости, проходящей через точку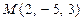 
параллельно плоскости 
.
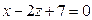6. Составить уравнение плоскости, проходящей:
6.1. Через ось Ox и точку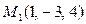 
.
6.2. Через ось Oy и точку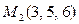 
.
6.3. Через ось Oz и точку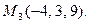 
7. Составить уравнение плоскости, параллельной:
7.1. Плоскости Oxz и проходящей через точку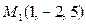 
.
7.2. Плоскости Oxy и проходящей через точку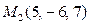 
.
7.3. Плоскости Oyz и проходящей через точку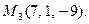 
8. При каких значениях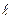 
и 
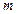следующие пары уравнений будут определять параллельные плоскости:
8.1.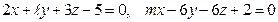 
.
8.2.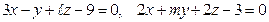 
.
8.3.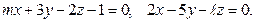 
9. Определить, при каком значении 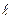следующие пары уравнений будут определять перпендикулярные плоскости:
9.1.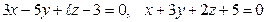 
.
9.2.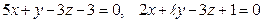 
.
9.3.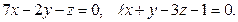 
10. Определить двугранные углы, образованные пересечением следующих пар плоскостей:
10.1.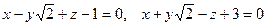 
.
10.2.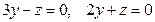 
.
10.3.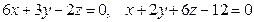 
.
10.4.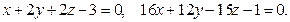 
11. Составить уравнение плоскости, проходящей через точку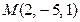 
перпендикулярно плоскостям 
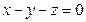и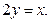 
12. Составить уравнение плоскости, проходящей через точк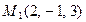и 
и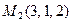 
параллельно вектору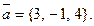 
13. Составить уравнение плоскости, проходящей через три точки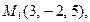 
.
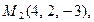
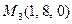14. Найти расстояние от точки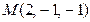 
до плоскости 
.
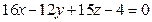15. Две грани куба лежат на плоскостях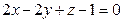 
и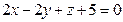 
. Вычислить объем этого куба.
16. Найти уравнение плоскости, проходящей через точк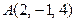и 
и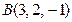 
перпендикулярной плоскости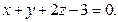 
17. Составить уравнение плоскости, проходящей через точку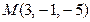 
и перпендикулярной плоскостям 
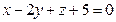и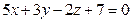 
.
Дополнительные задания
Д-1. Составить уравнение плоскости, проходящей через точку 
и перпендикулярной вектору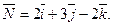 
Д-2. Найти уравнение плоскости, проходящей через точку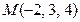 
параллельно плоскости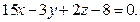 
Д-3. Из точки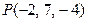 
на координатные плоскости опущены перпендикуляры. Составить уравнение плоскости, проходящей через их основания.
Д-4. Составить уравнение плоскости, проходящей через точку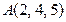 
и отсекающей равные отрезки на осях координат.
Д-5. Найти уравнение плоскости, точки которой одинаково удалены от точек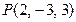 
и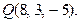 
Д-6. Составить уравнение плоскости, проходящей через точки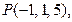 
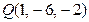и перпендикулярной плоскости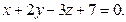 
Д-7. Составить уравнение плоскости, проходящей через точку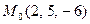 
параллельно векторам 
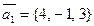и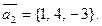 
Д-8. Являются ли параллельными плоскост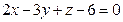и 
и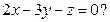 
Д-9. Являются ли перпендикулярными плоскости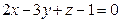 
, 
?
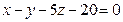Д-10. Вычислить расстояние между параллельными плоскостям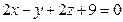и 
и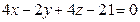 
.
Д-11. Найти расстояние от точки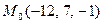 
до плоскости, проходящей через точк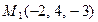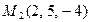и 
, 
и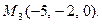 
Д-12. Какой угол образует с плоскостью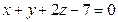 
вектор 
?
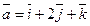Д-13. Вычислить угол между плоскостями, проходящими через точку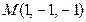 
, одна из которых содержит ось Ox, а другая — ось Oz.
Д-14. Найти уравнения плоскостей, проходящих через оси координат перпендикулярно плоскости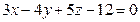 
.
Д-15. При каком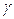 
плоскост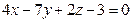и 
и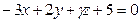 
перпендикулярны?
Д-16. Чему равна площадь треугольника, отсеченного плоскостью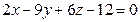 
от координатного угла Oxz?
Итоговый самоконтроль
С-1. Как составить уравнение плоскости, проходящей через заданную точку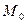 
параллельно двум векторам 
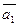и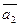 
?
С-2. Как составить уравнение плоскости, проходящей через три точки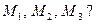 
С-3. Как проходит плоскость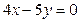 
?
С-4. При каких значениях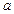 
и 
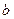плоскост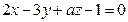и 
и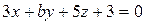 
параллельны?
С-5. Записать уравнение плоскости, проходящей через точку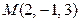 
перпендикулярно вектору 
.
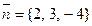С-6. При каком значении 
точка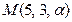 
лежит на плоскости 
?
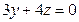С-7. Составить уравнение плоскости, проходящей через точку 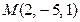параллельно плоскости 
.
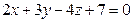С-8. Записать уравнение плоскости, проходящей через ось Oy и точку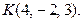 
С-9. При каком значении 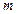плоскость 
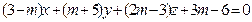проходит через начало координат?
С-10. Плоскость проходит через начало координат параллельно плоскости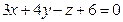 
. При каком значении 
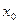точка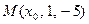 
будет лежать в этой плоскости?
С-11. Точка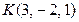 
является основанием перпендикуляра, опущенного из начала координат на плоскость. Найти ординату точки пересечения этой плоскости с осью Oy.
С-12. Найдите значение 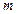, при котором острый угол между плоскостями 
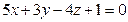и 
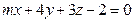равен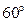 
.
С-13. Даны уравнения трех граней параллелепипеда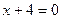 
, 
, 
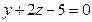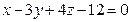и одна из его вершин 
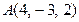. Найти уравнения трех других граней параллелепипеда.
С-14. Определить уравнение плоскости, проходящей через ось Oy и составляющей с плоскостью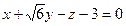 
угол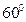 
.
С-15. Найти уравнение плоскости, отсекающей на отрицатель-
ной полуоси Oy отрезок, равный 4 и перпендикулярной вектору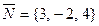 
.
С-16. Составить уравнение плоскости, проходящей через точку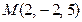 
и отсекающей на осях Ox и Oy втрое большие отрезки, чем на оси Oz.
С-17. Составить уравнение плоскости, расположенной на рас-
стоянии четырех единиц от плоскости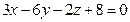 
и параллель-
но ей.
С-18. Написать уравнение плоскости, расположенной на равном расстоянии от двух данных параллельных плоскостей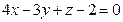 
и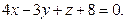 
Дата добавления: 2015-08-27; просмотров: 237 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Векторное и смешанное произведения векторов, их вычисление, свойства и применения | | | Уравнения прямой в . взаимное положение прямых, прямой и плоскости |