Читайте также:
|
1. Даны два вектора 
и 
. Определить проекции на координатные оси векторов:
1.1. 
. 1.2.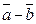 
. 1.3. 
.
1.4. 
. 1.5. 
. 1.6. 
.
2. Проверить коллинеарность векторов 
и 
. Установить, какой из них длиннее другого, во сколько раз? Сонаправлены ли они?
3. Найти длину вектора 
, его орт и направляющие косинусы.
4. Определить модули суммы и разности векторов 
и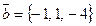 
.
5. Радиус-вектор точки М составляет с осью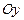 
угол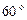 
, а с осью 
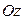— угол 
, его длина 
. Найти координаты точки М,
если ее абсцисса отрицательна.
6. Векторы 
, 
совпадают со сторонами 
. Определить координаты векторов, приложенных к вершинам треугольника и совпадающих с его медианами 
, 
и 
.
7. 
и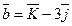 
. Определить длины диагоналей параллелограмма, построенного на векторах.
8. Даны модули векторов 
, 
, 
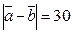. Определить 
.
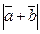9. Векторы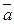 
и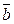 
образуют угол 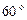, причем 
, 
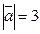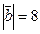. Определить 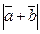и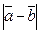 
.
10. Даны векторы 
, 
, 
. Разложить вектор 
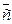по векторам 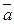и .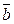
11. По данным векторам 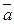и 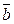построить векторы:
11.1. 
;
11.2. 
;
11.3. 
.
12. Выяснить, являются ли указанные векторы линейно зависимыми или линейно независимыми:
12.1.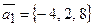 
, 
.
12.2. 
, 
.
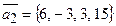12.3. 
, 
, 
.
13. Установить, образуют ли базис векторы 
, которые линейно выражаются через векторы 
:
13.1. 
, 
, 
;
, 
, 
.
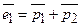13.2. 
, 
, 
;
, 
, 
.
13.3. 
, 
, 
;
, 
, 
.
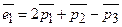13.4. , 
, 
;
, 
, 
.
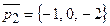13.5. 
, 
, 
;
, , 
.
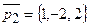14. Показать, что векторы образуют базис и найти в этом базисе координаты вектора 
:
14.1. 
, 
, 
.
14.2. 
, 
, 
.
14.3.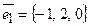 
, 
, 
.
14.4.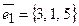 
, 
, 
.
14.5.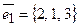 
, 
, 
.
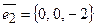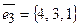Дополнительные задания
Д-1. Дан вектор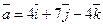 
. Найти вектор 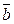, параллельный вектору 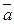и противоположно ему направленный, если 
.
Д-2. Дан вектор 
. Найти разложение вектора 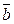по этому же базису, если вектор 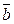параллелен вектору 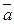, противоположно ему направлен и 
.
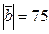Д-3. Построить векторы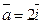 
, 
и 
. Разложить вектор 
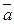по векторам и .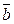
Д-4. Найти вектор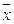 
, коллинеарный вектору 
, образующий с ортом 
острый угол и имеющий длину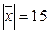 
.
Д-5. Доказать, что четырехугольник 
— ромб, если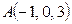 
, 
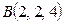, С (3, 5, 2), 
.
Д-6. Даны векторы 
и 
. Найти орт биссектрисы угла между 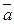и .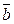
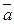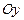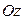Д-7. Вектор составляет с координатными осями и углы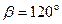 
, 
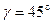, а с осью 
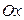тупой угол. Найти его координаты, если 
.
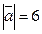Д-8. Известно, что равнобедренный. Найти координаты вершины С, если 
, 
, С 
. Сколько решений имеет задача?
Д-9. Даны вершины треугольника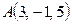 
, 
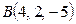, С(-4, 0, 3). Найти длину медианы, проведенной из вершины 
.
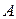Д-10. Определить, при каких значениях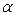 
и 
вектора 
и 
коллинеарны.
Д-11. Найти базисы системы векторов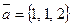 
, 
, 
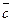={1.2.1}, 
, содержащие вектор .
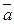Итоговый самоконтроль
С-1. Может ли вектор составлять с координатными осями углы 30, 120, 60o?
С-2. Следует ли из равенства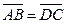 
равенство 
?
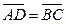С-3. Может ли угол между векторами быть равным 0, 30, 180, 175, 225o?
С-4. Каково взаимное расположение точек 
, если:
С-4.1. Векторы 
и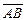 
коллинеарны. С-4,2. 
.
С-4.3. 
.
С-5. Какому условию должны удовлетворять векторы, чтобы они могли образовать плоскую фигуру?
С-6. Как следует направить векторы 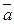и 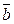, чтобы длина вектора была наибольшей? Наименьшей?
С-7. Какому условию удовлетворяют векторы 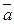и 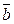, если:
С-7.1.. 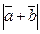> 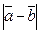. С-7.2. < .
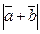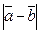С-7.3.. 
. С-7.4.. 
.
С-8. Система векторов содержит:
С-8.1. Два равных вектора.
С-8.2. Два пропорциональных вектора.
Является ли она линейно зависимой?
С-9. Известно, что 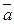, , 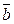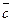линейно независимые векторы. Выяснить, линейно зависимы или линейно независимы векторы:
С-9.1. , ,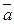 
. С-9.2. , 
, 
.
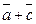С-9.3.. , , , 
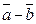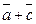. С-9.4. , 
, 
.
С-10. В треугольнике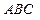 
проведена медиана 
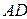. Какой вид имеет разложение вектора по векторам 
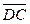и ?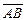
С-11. В параллелограмме 
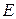— середина стороны 
. Найти разложение вектора 
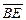по векторам 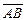и .
Дата добавления: 2015-08-27; просмотров: 126 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Собственные векторы и собственные значения матрицы | | | Скалярное произведение векторов, его вычисление, свойства и применения |