
Читайте также:
|
1. Решить матричным способом СЛУ:
1.1.  . 1.2.
. 1.2.  ;
;
1.3.  . 1.4.
. 1.4.  ;
;
1.5.  . 1.6.
. 1.6.  .
.
2. Решить матричное уравнение:
2.1.  . 2.2.
. 2.2.  ;
;
2.3.  . 2.4.
. 2.4.  .
.
2.5.  .
.
2.6.  .
.
3. Найти все матрицы, удовлетворяющие уравнению:
3.1.  . 3.2.
. 3.2. 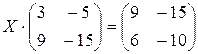 .
.
3.3.  . 3.4.
. 3.4.  .
.
3.5.  .
.
Дополнительные задания
Д-1. Решить СЛУ матричным способом:
Д-1.1. 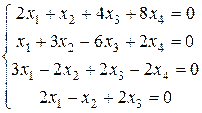 . Д-1.2.
. Д-1.2.  .
.
Д-1.3.  . Д-1.4.
. Д-1.4.  .
.
Д-1.5. 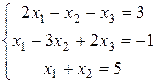 . Д-1.6.
. Д-1.6.  .
.
Д-2. Решить матричное уравнение:
Д-2.1. 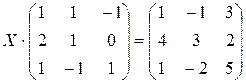 .
.
Д-2.2.  .
.
Д-2.3.  .
.
Д-2.4.  .
.
Д-2.5.  .
.
Д-3. Решить матричное уравнение:
 .
.
Д-4. Решить матричное уравнение:
Д-4.1. 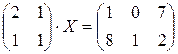 . Д-4.2.
. Д-4.2.  .
.
Д-4.3.  .
.
Итоговый самоконтроль
С-1. Может ли матричное уравнение иметь:
а) одно решение;
б) ни одного решения;
в) два решения.
Ответ поясните.
С-2. Может ли уравнение  иметь ненулевое решение?
иметь ненулевое решение?
С-3. Изменится ли решение СЛУ, если в основной матрице системы поменять местами две строки (два столбца)?
С-4. Верно ли, что:
а) если  , то
, то  ;
;
б) если  , то
, то  ;
;
в) если  , то
, то  .
.
С-5.  матричная форма записи системы линейных уравнений. Какое из выражений
матричная форма записи системы линейных уравнений. Какое из выражений 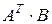 ,
,  ,
,  является решением системы?
является решением системы?
С-6. Решить матричные уравнения:
а)  ; б)
; б)  .
.
С-7. Можно ли говорить о сходстве решения СЛУ матричным способом и по формулам Крамера?
С-8. Решить матричное уравнение:
а)  б)
б) 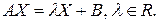
Дата добавления: 2015-08-27; просмотров: 83 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Линейные операции над матрицами. Умножение матриц. Обратная матрица | | | Решение систем линейных уравнений методом Гаусса. |