
|
Читайте также: |
1. Найти матрицу, заданную условием:
1.1.  , если
, если 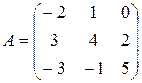 ,
,  .
.
1.2. 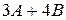 , если
, если  ,
,  .
.
1.3. 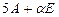 , если
, если  .
.
2. Найти значение матричного многочлена  , если:
, если:
2.1.  ,
,  .
.
2.2.  ,
,  .
.
3. Проверить перестановочность матриц:
3.1.  ,
, 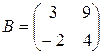 .
.
3.2.  ,
,  .
.
4. Найти произведение  и
и  . Существуют ли матрицы
. Существуют ли матрицы  ?
?
4.1. 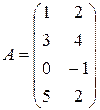 . 4.2.
. 4.2.  . 4.3.
. 4.3.  .
.
5. Привести матрицы к ступенчатому виду:
5.1.  . 5.2.
. 5.2.  .
.
5.3.  .
.
6. Найти матрицу, обратную данной:
6.1.  . 6.2.
. 6.2. 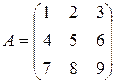 . 6.3.
. 6.3. 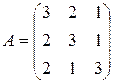 .
.
7. Найти обратную матрицу методом элементарных преобразований:
7.1.  . 7.2.
. 7.2. 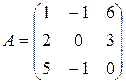 7.3.
7.3.  .
.
7.4.  . 7.5.
. 7.5. 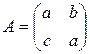 .
.
Дополнительные задания
Д-1. Найти произведения  и
и 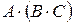 :
:
Д-1.1.  ,
,  ,
, 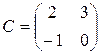 .
.
Д-1.2.  ,
,  ,
,  .
.
Д-2. Найти матрицы  и
и  :
:
Д-2.1.  .
.  .
.  .
.
Д-2.2.  .
. 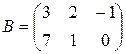 .
.  .
.
Д-3. Найти матрицу  :
:
Д-3.1. 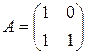 . Д-3.2.
. Д-3.2.  . Д-3.3.
. Д-3.3.  .
.
Д-4. Найти  , если
, если 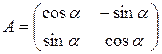 .
.
Д-5. Найти матрицы, перестановочные с матрицей  , если:
, если:
Д-5.1.  . Д-5.2.
. Д-5.2.  . Д-5.3.
. Д-5.3.  .
.
Д-6. Найти матрицу, обратную данной, с помощью присоединенной матрицы или методом элементарных преобразований:
Д-6.1.  . Д-6.2.
. Д-6.2. 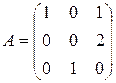 . Д-6.3.
. Д-6.3.  .
.
Д-6.4.  . Д-6.5.
. Д-6.5. 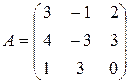 . Д-6.6
. Д-6.6 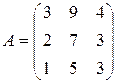 .
.
Д-7. Вычислить матрицу  , где
, где  ,
,
 ,
,  .
.
Д-8. Вычислить матрицу 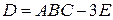 , где
, где  ,
,  ,
, 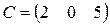 .
.
Д-9. Вычислить  , если
, если  .
.
Д-10. Найти 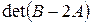 , если
, если  ,
,  .
.
Д-11. При каких значениях l матрица  не имеет обратной?
не имеет обратной?
Д-11.1.  . Д-11.2.
. Д-11.2.  . Д-11.3.
. Д-11.3.  .
.
Итоговый самоконтроль
С-1. Следует ли из возможности сложения матриц возможность их перемножить и наоборот?
С-2. Можно ли умножить и в любом ли случае:
а) матрицу-столбец на матрицу  ;
;
б) матрицу  на матрицу-столбец;
на матрицу-столбец;
в) матрицу-строку на матрицу  ;
;
г) матрицу  на матрицу-строку;
на матрицу-строку;
д) матрицу-строку на матрицу-столбец;
е) матрицу-столбец на матрицу-строку.
С-3. Можно ли найти квадрат матрицы, имеющей размеры  ?
?
С-4. Каковы размеры матрицы  , если известно, что
, если известно, что  ?
?
С-5. Можно ли утверждать, что  ?
?
С-6. Можно ли при умножении прямоугольных матриц получить квадратную матрицу?
С-7. Можно ли утверждать, что  ?
?
С-8. Верно ли утверждение  ?
?
С-9. Верно ли утверждение: матрица, у которой пропорциональны соответственные элементы всех строк, эквивалентна нулевой?
С-10. Назовите наименьший размер матрицы.
С-11. Изменится ли произведение матриц при транспонировании одной из них?
С-12. Верно ли утверждение, что  ?
?
С-13. Какие размеры имеет матрица, обратная матрице размера  ?
?
С-14. Как изменится матрица 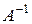 , если в матрице
, если в матрице  поменять местами две строки (столбца)?
поменять местами две строки (столбца)?
С-15. Изменится ли матрица 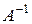 , если матрицу
, если матрицу  умножить на число
умножить на число  ?
?
С-16. Как изменится матрица 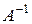 , если столбец или строку матрицы
, если столбец или строку матрицы  умножить на число
умножить на число  ?
?
С-17. Является ли верным равенство:
а)  ; б)
; б)  ;
;
в) 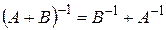 ; г)
; г)  .
.
С-18. Каким общим свойством обладают матрицы  и
и  ?
?
Дата добавления: 2015-08-27; просмотров: 103 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление определителей. Решение систем линейных уравнений по формулам Крамера | | | Решение систем линейных уравнений матричным способом. Решение матричных уравнений |