Уравнения прямой в . взаимное положение прямых, прямой и плоскости

1. Составить параметрические уравнения прямой, проходящей через точку параллельно:

1.1. Вектору . 1.2. Прямой .

1.3. Оси Ох. 1.4. Оси оу. 1.5. Оси Оz.

2. Даны вершины треугольника A (3, 6, −7), B (−5, 2, 3) и C (4, −7, −2). Составить канонические уравнения его медианы, проведенной из верши-
ны C.

3. Найти координаты какой-либо точки, лежащей на прямой .

Составить канонические уравнения прямой.

4. Лежит ли точка (1, 4, −2) на прямой 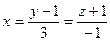? Найти координаты какой-либо точки на этой прямой.

5. Доказать параллельность прямых и .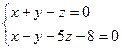

6. Найти угол между прямым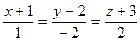и и .

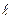7. Даны прямые , . При каком значении они пересекаются? Найти точку K пересечения прямых при полученном значении .

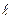8. Найти точку пересечения прямой и плоскости .

9. Составить уравнение плоскости, проходящей через точку перпендикулярно прямой .

10. Составить уравнения прямой, проходящей через точку перпендикулярно плоскости .

11. При каком значении m прямая параллельна плоскости ?

12. При каких значениях A и D прямая лежит
в плоскости .

13. Найти проекцию точки P (2, −1, 3) на прямую .

14. Найти точку Q, симметричную точку P (1, 3, − 4) относительно плоскости .

15. Определить угол между прямой и плоскостью .

16. Найти расстояние между параллельными прямым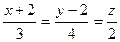и и .

Дополнительные задания

Д-1. Записать канонические уравнения прямой, проходящей через точки и .

Д-2. Даны вершины треугольника A (3, −1, −1), B (1, 2, −7) и C (−5, 14, −3). Составить канонические уравнения биссектрисы его внутреннего угла при вершине B.

Д-3. Доказать перпендикулярность прямых и .

Д-4. Найти проекцию точки A (3, −1, 2) на плоскость .

Д-5. Составить уравнение плоскости, проходящей через точку K (−3, 1, 2) и через прямую .

Д-6. Составить уравнение плоскости, проходящей через две параллельные прямые и .

Д-7. Найти уравнение плоскости, проектирующей прямую 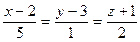на плоскость .

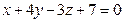Д-8. При каких значениях A и B плоскость 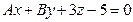перпендикулярна к прямой ?

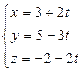Д-9. Найти точку Q, симметричную точке P (4, 1, 6) относительно прямой .

Д-10. Вычислить расстояние d от точки P (2, 3, −1) до прямой .

Д-11. Доказать, что прямые и 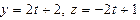лежат в одной плоскости и составить уравнение этой плоскости.

Д-12. Составить уравнение плоскости, проходящей через перпендикуляры, опущенные из точки A (3, −2, 8) на плоскости
и .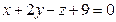

Д-13. Через прямую 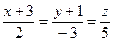провести плоскость, параллельную прямой .

Д-14. Составить параметрические уравнения прямой, проходящей через точки пересечения плоскости с прямыми и .

Д-15. Убедившись, что прямые и параллельны, вычислить расстояние между ними.

Д-16. Найти точку Q, симметричную точке P (3, −4, −6) относите-
льно плоскости, проходящей через точки ,
и .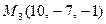

Д-17. Найти кратчайшее расстояние между скрещивающимися прямыми и .

Итоговый самоконтроль

C-1. При каких значениях m и n прямая и плоскость взаимно перпендикулярны?

С-2. Какой угол с осью Oy образует направляющий вектор прямой ?

С-3. Чему равна величина , если — точка пересечения прямой с плоскостью ?

С-4. Составить уравнение прямой, проходящей через точку параллельно вектору .

С-5. При каком значении m прямая параллельна плоскости ?

С-6. Найдите меньший угол (в градусах) между прямым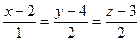и и .

С-7. Найти сумму координат точки пересечения прямой
с плоскостью .

С-8. Найдите острый угол (в градусах) между прямыми и .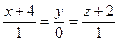

С-9. Плоскость проходит через точку и через прямую . Найти абсциссу точки пересечения ее с осью Ox.

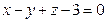С-10. Точка является проекцией точки на плоскость . Найти значение .

С-11. При каком значении B плоскость параллельна прямой .

С-12. При каких значениях A и B плоскость 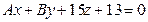перпендикулярна прямой .

С-13. Найти уравнение проекции прямой на плоскость .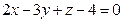

С-14. Лежит ли прямая в плоскости ?

С-15. При каком значении A плоскость параллельна прямой .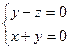

С-16. Дана прямая . Как по отношению к ней расположены прямые:

16.1. . 16.2. .

Дата добавления: 2015-08-27