Читайте также:
|
1. Проверить, лежат ли на прямой 
точки 
.
2. Определить точки пересечения прямой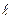 
с осями координат и построить эти прямые:
2.1. 4 х + 3 у - 12 = 0 2.2. -2 х + 5 у + 20 = 0
3. Доказать параллельность прямых:
3.1. 3 х + 5 у – 4 = 0 и 6 их + 10 у + 7 = 0
3.2. 2 х - 1 = 0 и х + 3 = 0
4. Из пучка прямых с центром в точке 
выделить прямую:
4. 1. Параллельную прямой 
.
4. 2. Перпендикулярную прямой 
.
4. 3. Проходящую через точку 
.
5. Определить угол, образованный прямыми:
5. 1. 
.
5. 2. 
.
5. 3. 
.
6. При каких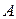 
и 
параллельны прямые:
6. 1.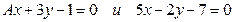 
.
6. 2. 
.
7. Дана прямая 
. Составить уравнение прямой, проходящей через точку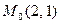 
:
7. 1. Параллельно данной прямой.
7. 2. Перпендикулярно данной прямой.
8. Даны уравнения двух сторон прямоугольника 
и уравнение одной из его диагоналей 
. Составить уравнения двух других сторон прямоугольника.
9. Найти точку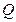 
, симметричную точке 
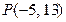относительно прямой 
.
10. Даны вершины треугольника 
. Составить уравнение перпендикуляра, опущенного из вершины 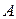на медиану, проведенную из вершины .
11. Точка 
является вершиной квадрата, диагональ которого лежит на прямой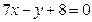 
. Составить уравнения сторон и второй диагонали этого квадрата.
12. Составить уравнение прямой, которая проходит через точку 
и отсекает от координатного угла треугольник с площадью,
равной 150.
13. Точка 
является вершиной квадрата, одна из сторон
которого лежит на прямой 
. Вычислить площадь этого квад-
рата.
14. Найти площадь треугольника, заключенного между осями координат и прямой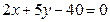 
.
15. Составить уравнения перпендикуляров к прямой 
в точках ее пересечения с осями координат.
16. Составить уравнение прямой, проходящей через точку пере-
сечения прямых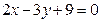 
, 
перпендикулярно прямой
.
17. Даны координаты середин сторон треугольника: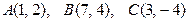 
. Найти уравнения прямых, на которых лежат стороны треугольника.
18. Даны уравнения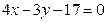 
и 
двух сторон квадрата и одна из его вершин 
. Найти уравнения прямых, на которых лежат две другие стороны квадрата.
19. Найти уравнение прямой, параллельной прямой 
и отстоящей от нее на расстоянии 3 единицы.
Дополнительные задания
Д-1. Каков угловой коэффициент прямой 
? Какой угол (острый или тупой) образует эта прямая с осью Ох?
Д-2. Среди прямых указать параллельные и перпендикулярные:
.
Д-3. Дана прямая: 
. Какой угловой коэффициент будут иметь параллельная и перпендикулярная ей прямые?
Д-4. Даны уравнения двух сторон прямоугольника 
, 
и одна из его вершин . Составить уравнения двух других сторон этого прямоугольника.
Д-5. Найти проекцию точки 
на прямую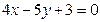 
.
Д-6. Даны вершины треугольника 
. Составить уравнения его высот.
Д-7. Составить уравнения прямых, проходящих через вершины треугольника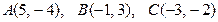 
параллельно противоположным сторонам.
Д-8. Даны уравнения двух сторон прямоугольника 
, 
и одна из его вершин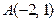 
. Вычислить площадь этого прямоугольника.
Д-9. Составить уравнение перпендикуляра, проведенного к отрезку 
через его середину, если 
и 
.
Д-10. Составить уравнение перпендикуляра, опущенного из точки 
на прямую, отсекающую на осях Ох и Оy соответственно отрезки 5
и –3.
Д-11. Составить уравнение прямой, проходящей через точку пересечения прямых 
, 
параллельно оси Ох; параллельно оси Оy.
Д-12. Найти точку пересечения медиан треугольника, вершинами которого являются точки 
.
Д-13. Найти точку 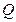, симметричную точке 
относительно прямой, проходящей через точки 
и 
.
Д-14. Даны вершины треугольника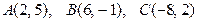 
. Найти угол между высотой 
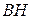и медианой 
.
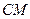Д-15. Написать уравнения сторон треугольника, зная одну его вершину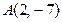 
, а также уравнения высоты 
и медианы 
, проведенных из различных вершин.
Д-16. Даны две вершины 
и точка 
пересечения высот треугольника. Составить уравнения его сторон.
Д-17. Даны уравнения двух сторон треугольника: 
и 
. Его медианы пересекаются в точке 
. Составить уравнение третьей стороны треугольника.
Итоговый самоконтроль
С-1. Записать уравнение прямой, проходящей через начало координат параллельно прямой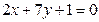 
.
С-2. От параметрических уравнений прямой 
перейти к общему уравнению прямой.
С-3. Даны точки 
, 
и прямая 
. Составить уравнение прямой проходящей через середину отрезка 
перпендикулярно заданной прямой.
С-4. Вычислить угловой коэффициент прямой:
С-4.1. Отсекающей на осях Ох и Оy соответственно отрезки 
С-4.2. Проходящей через точки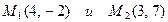 
.
С-5. Найти площадь треугольника, образованного прямой 
и осями координат.
С-6. Определить при каких значениях a прямые 
и 
параллельны.
С-7. Выяснить при каком значении B вектор 
является направляющим вектором прямой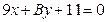 
.
С-8. Найти наибольшее значение А, при котором расстояние от начала координат до прямой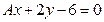 
равно 2.
С-9. Даны вершины треугольника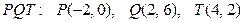 
. Вектор 
является вектором нормали медианы этого треугольника, проведенного из вершины 
. Найти значение «k».
C-10. Даны вершины треугольника 
. Найти:
C-10.1. Уравнения сторон 
и 
.
C-10.2. Уравнение высоты, проведенной из точки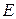 
.
C-10.3. Уравнение медианы, проведенной из точки 
.
C-10.4. Длину этой медианы.
C-10.5. Уравнение биссектрисы.
C-10.6. Величину внутреннего угла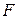 
.
С-11. Даны уравнения боковых сторон равнобедренного треугольника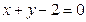 
, 
и точка (3, 5) на его основании. Найти уравнение прямой, на которой лежит основание.
Дата добавления: 2015-08-27; просмотров: 281 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Уравнения прямой в . взаимное положение прямых, прямой и плоскости | | | Кривые второго порядка |