Аналитические способы решения прямых задач гравиразведки.

Аномалия силы тяжести, вызванная притяжением тел известной формы, размера и плотности, может быть вычислена на основании закона всемирного притяжения (закон Ньютона).

Пусть в координатной системе xyz ось z направлена вниз к центру Земли. Ставится задача определить в точке наблюдения А (x,y,z) аномальную силу тяжести (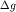), т.е. вертикальную составляющую силы притяжения Землей единицы массы () элементарной массой dm, находящейся в точке M (x',y',z') (рис. 1.2).

Рис.1.2 К определению аномалий силы тяжести от элементарной массы

По закону Ньютона притяжение единичной массы равно:

f=Gdm/r²,

где - гравитационная постоянная, - расстояние между точками (см. 1.4).

Аномалия 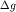является проекцией вектора f на ось z:

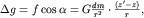
(1.6)

где из треугольника ABM . Это же выражение можно получить с помощью потенциала W=Gdm/r. В самом деле:

(1.7)

Обозначив плотность притягивающей массы через , а ее объем через dV, можно записать

(1.8)

Такова будет аномалия силы тяжести, обусловленная массой, расположенной в пустоте. В природных условиях аномальные включения расположены во вмещающей среде с некоторой плотностью , поэтому под массой dm надо понимать избыточную массу .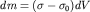

Отсюда

(1.9)

где - избыточная плотность.

При 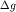имеет положительный знак, т.е. наблюдается увеличение притяжения и положительные аномали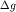и . При 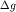имеет отрицательный знак, т.е. наблюдается уменьшение притяжения и отрицательные аномалии .

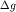В принципе аномалия, созданная любым телом, может быть определена интегралом по объему тела:

(1.10)

т.е. суммой притяжений всех элементарных объемов, из которых состоит тело.

Рассмотрим несколько прямых и обратных задач для тел простой геометрической формы.

Дата добавления: 2015-08-26