Прямая и обратная задачи над шаром.

1. Прямая задача. Пусть однородный шар радиуса и плотности расположен на глубине 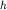в среде с плотностью (для простоты центр находится на оси z, а наблюдения проводятся по оси x в точке P) (рис. 1.3).

Рис.1.3 Гравитационное поле шара

Формула для вычисления может быть получена из (1.6) - (1.9) путем замены элемента массой шара в силу того, что притяжение однородным шаром происходит так, как если бы вся масса была сосредоточена в центре шара. Учтя, что x'=y'=0, z'=h, y=z=0, получим для шара

(1.11)

График 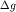будет иметь максимум над шаром (x =0) и асимптотически стремиться к нулю при удалении от шара. В плане изолинии 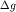будут иметь вид концентрических окружностей.

Вторая производная (градиент аномалии по профилю наблюдений) равна:

Вид кривой W_xz может быть легко получен путем графического построения из кривой 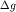. График W_xz имеет перед шаром максимум, за шаром - минимум, над центром шара - ноль.

2. Обратная задача. Из (1.11) максимум 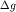над центром шара (x =0) равен .

Для точки, удаленной от максимума на расстояние x_1/2, имеющей , можно записать следующее уравнение:

Решив последнее уравнение, получим формулу для определения глубины залегания центра шара h=1,3x_1/2. Зная 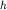, легко найти избыточную массу (): .

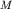Так как 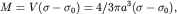то, зная избыточную плотность , можно рассчитать объем (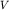) и радиус шара (). Так, радиус равен:

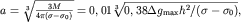
где 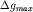- в миллигалах, 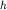- в метрах, - в тоннах / куб. метр (г/см³).

Дата добавления: 2015-08-26