
Читайте также:
|
1. Прямая задача. Рассмотрим бесконечно длинный круговой горизонтальный цилиндр радиуса 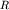 , расположенный вдоль оси y (рис. 1.4). Ось наблюдений (x) направим вкрест простирания цилиндра.
, расположенный вдоль оси y (рис. 1.4). Ось наблюдений (x) направим вкрест простирания цилиндра.
|
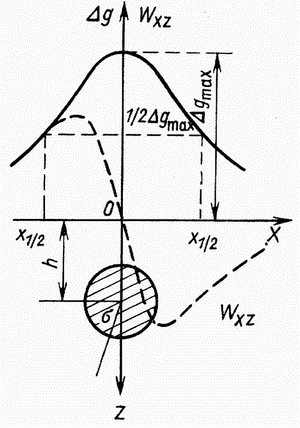
| Рис.1.4 Гравитационное поле бесконечно длинного кругового горизонтального цилиндра |
Притяжение однородным цилиндром происходит так же, как если бы вся его масса была сосредоточена вдоль вещественной линии, расположенной вдоль оси цилиндра, с массой единицы длины, равной  . Используя (1.10), можно получить формулы для
. Используя (1.10), можно получить формулы для 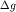 и
и  :
:

| (1.12) |
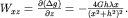
|
Графики 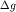 и
и  над цилиндром и шаром внешне похожи (см. рис. 1.3 и 1.4). В плане изолинии
над цилиндром и шаром внешне похожи (см. рис. 1.3 и 1.4). В плане изолинии 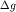 над цилиндром будут вытянутыми параллельными линиями.
над цилиндром будут вытянутыми параллельными линиями.
2. Обратная задача. Из (1.10 и 1.12) можно при х =0 получить  . Отсюда
. Отсюда
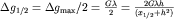
|
и  ,
,  , т.е. глубина залегания цилиндра равна расстоянию от точки максимума
, т.е. глубина залегания цилиндра равна расстоянию от точки максимума 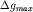 до точки, где
до точки, где  .
.
Определив 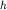 и зная избыточную плотность, можно рассчитать
и зная избыточную плотность, можно рассчитать

|
и радиус цилиндра:

|
Зная 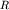 , можно получить глубины залегания верхней hв=h-R и нижней hн=h+R кромок цилиндра. Нетрудно вычислить выражение и для
, можно получить глубины залегания верхней hв=h-R и нижней hн=h+R кромок цилиндра. Нетрудно вычислить выражение и для  .
.
Дата добавления: 2015-08-26; просмотров: 91 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Прямая и обратная задачи над шаром. | | | Прямая и обратная задача над вертикальным уступом (сбросом). |