|
Читайте также: |
1. Прямая задача. Пусть вертикальный уступ (сброс) простирается бесконечно вдоль оси y (рис. 1.5). Наблюдения производятся вдоль оси (x), (y=z=0), расположенной вкрест простирания сброса. Если глубина до кровли z1 и z2, а амплитуда уступа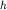 
, то, согласно (1.10),
| (1.13) |
В общем случае выражение интеграла имеет громоздкий вид. В частности, полная максимальная аномалия над уступом (разность силы тяжести между поднятым и опущенным крылом) определится следующей формулой:
| (1.14) |
Над уступом (x =0) аномалия равна половине максимальной.
|
| Рис.1.5 Гравитационное поле над уступом (сбросом) |
2. Обратная задача. Из (1.14) можно определить 
В теории гравиразведки доказано, что примерная глубина расположения середины высоты уступа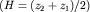 
равна 
т.е. абсциссе точки, в которой 
где 
- аномалия над уступом, а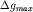 
- полная аномалия. Практически для определения 
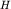на кривой 
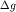находится местоположение сброса 
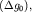и в масштабе профиля рассчитывается 
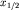- расстояние от сброса до точки, в которой 
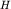Зная и 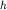, легко определить глубины до приподнятого 
и опущенного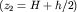 
крыла.
Дата добавления: 2015-08-26; просмотров: 93 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Прямая и обратная задачи над горизонтальным бесконечно длинным круговым цилиндром. | | | Графическое определение аномалии силы тяжести двухмерных тел с помощью палетки Гамбурцева. |