
Читайте также:
|
1. Составить уравнение окружности в каждом из следующих слу-
чаев:
1.1. Центр окружности совпадает с точкой  и радиус R = 7.
и радиус R = 7.
1.2. Окружность проходит через точку  и ее центр совпадает с точкой
и ее центр совпадает с точкой 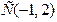 .
.
1.3. Точки  и
и  являются концами одного из диаметров окружности.
являются концами одного из диаметров окружности.
1.4. Центр окружности совпадает с точкой 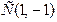 и прямая
и прямая  является касательной к окружности.
является касательной к окружности.
2. Какие из нижеприводимых уравнений определяют окружности? Найти центр C и радиус R каждой из них:
2.1. 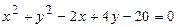 . 2.2.
. 2.2.  .
.
2.3.  . 2.4.
. 2.4.  .
.
3. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:
3.1. Его большая ось равна 10, а расстояние между фокусами 2 с = 8.
3.2. Расстояние между его фокусами 2с=6 и эксцентриситет  .
.
3.3. Расстояние между его директрисами равно 5 и расстояние между фокусами 2 с = 4.
4. Дан эллипс  . Найти:
. Найти:
4.1. Е го полуоси. 4.2. Фокусы.
4.3. Эксцентриситет. 4 4. Уравнения директрис.
5. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:
5.1. Расстояние между фокусами 2с=6 и эксцентриситет 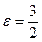 .
.
5.2. Ось 2а = 16 и эксцентриситет  .
.
5.3. Уравнения асимптот  и расстояние между фокусами 2 с = 20.
и расстояние между фокусами 2 с = 20.
6. Дана гипербола  . Найти:
. Найти:
6.1. Полуоси a и b. 6.2. Фокусы.
6.3. Эксцентриситет. 6.4. Уравнения асимптот.
6.5. Уравнения директрис.
7. Составить уравнение параболы, вершина которой находятся в начале координат, зная, что парабола расположена:
7.1. В правой полуплоскости симметрично относительно оси Ох, и ее параметр p = 3.
7.2. В левой полуплоскости симметрично относительно оси Ох и ее параметр p = 0,5.
7.3. В верхней полуплоскости симметрично относительно оси Оy и ее параметр p =  .
.
7.4. В нижней полуплоскости симметрично относительно оси Оy и ее параметр p = 3.
8. Определить величину параметра и расположение относительно координатных осей следующих парабол:
8.1.  . 8.2.
. 8.2. 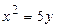 .
.
8.3.  . 8.4.
. 8.4. 
9. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты ее вершины А и величину параметра p:
9.1. 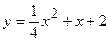 . 9.2.
. 9.2. 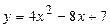 .
.
9.3.  .
.
10. Фокусы гиперболы совпадают с фокусами эллипса  . Составить уравнение гиперболы, если ее эксцентриситет
. Составить уравнение гиперболы, если ее эксцентриситет  .
.
11. Составить уравнение и построить линию, расстояние каждой точки которой от точки  вдвое меньше ее расстояния от прямой
вдвое меньше ее расстояния от прямой 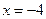 .
.
12. Составить уравнение и построить линию, расстояние каждой точки которой от точки  и от прямой y =
и от прямой y =  относятся как 5: 4.
относятся как 5: 4.
13. Составить уравнение и построить линию, каждая точка которой одинаково удалена от точки  и от прямой
и от прямой  .
.
14. По каноническому уравнению кривой второго порядка определить тип кривой, начертить ее график. Найти координаты фокусов и центра, полуоси:
14.1. 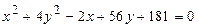 .
.
14.2.  .
.
14.3.  .
.
14.4.  .
.
14.5.  .
.
14.6.  .
.
Дополнительные задания
Д-1. Составить уравнение окружности в каждом из следующих
случаев:
Д-1.1. Окружность проходит через начало координат и ее центр совпадает с точкой  .
.
Д-1.2. Окружность проходит через точку  и
и  , а ее центр лежит на прямой
, а ее центр лежит на прямой  .
.
Д-2. Установить, какие линии определяются следующими уравне-
ниями:
Д-2.1.  . Д-2.2.
. Д-2.2.  .
.
Д-2.3.  . Д-2.4.
. Д-2.4.  .
.
Д-3. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная что:
Д-3.1. Его полуоси равны 5 и 2.
Д-3.2. Его малая ось равна 24, а расстояние между фокусами 2с = 10.
Д-3.3. Его большая ось равна 8, а расстояние между директрисами равно 16.
Д-4. Дан эллипс  . Найти на эллипсе точки, абсцисса которых равна −3.
. Найти на эллипсе точки, абсцисса которых равна −3.
Д-5. Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны:
Д-5.1. Точки 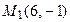 и
и 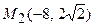 гиперболы.
гиперболы.
Д-5.2. Точка 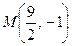 гиперболы и уравнения асимптот
гиперболы и уравнения асимптот  .
.
Д-5.3. Уравнения асимптот  и уравнения директрис
и уравнения директрис  .
.
Д-6. Составить уравнение гиперболы, фокусы которой лежат в вершинах эллипса  , а директрисы проходят через фокусы этого
, а директрисы проходят через фокусы этого
эллипса.
Д-7. Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена симметрично
Д-7.1. Оси Ох и проходит через точку 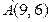 .
.
Д-7.2. Оси Ох и проходит через точку  .
.
Д-7.3. Оси Оy и проходит через точку  .
.
Д-7.4. Оси Оy и проходит через точку 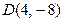 .
.
Д-8. Найти фокус F и уравнение директрисы параболы  .
.
Д-9. Составить уравнение и построить линию, расстояния каждой точки которой от точки 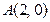 и от прямой
и от прямой  относятся, как 4: 5.
относятся, как 4: 5.
Д-10. Составить уравнение эллипса, проходящего через точки  и
и  .
.
Д-11. В эллипс  вписан правильный треугольник, одна из вершин которого совпадает с правой вершиной эллипса. Найти координаты двух других вершин треугольника.
вписан правильный треугольник, одна из вершин которого совпадает с правой вершиной эллипса. Найти координаты двух других вершин треугольника.
Д-12. В эллипс  вписан квадрат так, что его стороны параллельны осям эллипса. Найти площадь квадрата.
вписан квадрат так, что его стороны параллельны осям эллипса. Найти площадь квадрата.
Д-13. Чему равен периметр четырехугольника, вершины которого совпадают с вершинами эллипса  .
.
Д-14. Составить уравнения асимптот гиперболы  , построить ее.
, построить ее.
Д-15. Дан эллипс 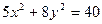 . Найти уравнение гиперболы, вершины которой находятся в фокусах, а фокусы — в вершинах данного эллипса.
. Найти уравнение гиперболы, вершины которой находятся в фокусах, а фокусы — в вершинах данного эллипса.
Д-16. Найти координаты такой точки параболы  , которая находится от директрисы на расстоянии 3,5.
, которая находится от директрисы на расстоянии 3,5.
Д-17. Найти уравнение прямой, которая проходит через вершину параболы  параллельно прямой
параллельно прямой 
Итоговый самоконтроль
С-1. Пусть уравнение  определяет кри-
определяет кри-
вую второго порядка. Какой будет эта кривая, если 
С-2. Определите эксцентриситет эллипса  .
.
С-3. Каково межфокусное расстояние гиперболы  .
.
С-4. Найдите угловой коэффициент прямой, проходящей через точку  и через вершину параболы
и через вершину параболы  .
.
С-5. Через фокусы параболы  проведена хорда, перпендикулярная ее оси. Чему равна длина этой хорды.
проведена хорда, перпендикулярная ее оси. Чему равна длина этой хорды.
С-6. Как можно определить эллипс, гиперболу, используя понятие эксцентриситета?
С-7. Чему равен эксцентриситет земного меридиана, имеющего форму эллипса, отношение осей которого равно  .
.
С-8. Чему равен эксцентриситет эллипса, у которого малая ось равна расстоянию между фокусами.
С-9. Найти площадь треугольника, образованного асимптотами гиперболы  и прямой
и прямой 
С-10. Найти эксцентриситет гиперболы, асимптота которой составляет с действительной осью угол  .
.
С-11. Найти фокальные радиусы точки 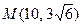 , лежащей на гиперболе
, лежащей на гиперболе 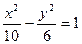 . Найти расстояние от точки
. Найти расстояние от точки  до директрис.
до директрис.
С-12. Проходит ли гипербола  через точки
через точки 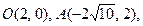

С-13. Чему равен угол между асимптотами гиперболы  ?
?
С-14. Составить уравнение гиперболы, зная ее эксцентриситет  , фокус
, фокус  и уравнение соответствующей директрисы
и уравнение соответствующей директрисы  .
.
С-15. Дана парабола  Найти длину ее хорды, проходящей через точку
Найти длину ее хорды, проходящей через точку  перпендикулярно прямой
перпендикулярно прямой 
С-16. Каково будет уравнение параболы  , если ее ось симметрии повернуть на
, если ее ось симметрии повернуть на  ? На
? На 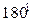 ? На
? На  ?
?
С-17. Каково уравнение параболы с вершиной в точке (0, 0), если уравнение ее директрисы 
С-18. Какое уравнение гиперболы является более общим: каноническое  или известное из школы
или известное из школы 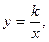 где
где  ?
?
Действительные и комплексные числа
1. Представить в тригонометрической и показательной формах комплексные числа. Изобразить число в комплексной плоскости, отметить на рисунке его модуль и аргумент.
1.1.  . 1.2. −
. 1.2. −  . 1.3.
. 1.3. 
1.4. 5. 1.5. −10. 1.6. 
2. Записать в алгебраической форме:
2.1.  . 2.2.
. 2.2.  . 2.3.
. 2.3.  .
.
3. Найти модуль и главное значение аргумента комплексных чисел:
3.1. 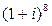 . 3.2.
. 3.2.  . 3.3.
. 3.3. 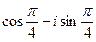 .
.
3.4. 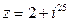 . 3.5.
. 3.5. 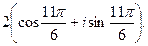
4. Записать комплексное число в алгебраической форме:
4.1.  . 4.2.
. 4.2.  . 4.3.
. 4.3.  .
.
4.4.  4.5.
4.5. 
5. Решить квадратное уравнение:
5.1. 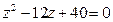 . 5.2.
. 5.2.  .
.
5.3.  . 5.4.
. 5.4. 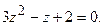
6. Найти все значения корней и построить их на комплексной плоскости:
6.1.  . 6.2.
. 6.2.  . 6.3.
. 6.3. 
7. Решить уравнения:
7.1.  . 7.2.
. 7.2.  . 7.3.
. 7.3.  .
.
7.4. 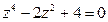 . 7.5.
. 7.5. 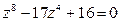 . 7.6.
. 7.6. 
8. Выполните арифметические действия над комплексными числами  Изобразите найденные числа на комплексной плоскости.
Изобразите найденные числа на комплексной плоскости.
9. Изобразить на рисунке множества точек z комплексной плоскости, удовлетворяющих условию:
9.1. 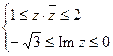 . 9.2.
. 9.2.  .
.
9.3.  . 9.4.
. 9.4. 
Дополнительные задания
Д-1. Найти действительную и мнимую части комплексных чисел:
Д-1.1. 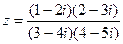 . Д-1.2.
. Д-1.2.  . Д-1.3.
. Д-1.3. 
Д-2. Найти модуль и главное значение аргумента  комплексных чисел:
комплексных чисел:
Д-2.1.  . Д-2.2.
. Д-2.2.  .
.
Д-3. Выполните арифметические действия над комплексными числами. Изобразите найденные числа на комплексной плоскости:
Д-3.1.  . Д-3.2.
. Д-3.2.  .
.
Д-3.3. 
Д-4. Изобразить множество всех точек комплексной плоскости, удовлетворяющих данным неравенствам
Д-4.1.  . Д-4.2.
. Д-4.2. 
Д-5. Изобразить область, заданную неравенствами 
Д-6. Замкнутое множество, изображенное на рисунке, задать системой неравенств

Д-7. Выполнить действия. Результат представить в алгебраической
форме:
Д-7.1.  . Д-7.2.
. Д-7.2. 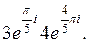
Д-8. Решить уравнения:
Д-8.1.  . Д-8.2.
. Д-8.2. 
Д-9. Решить систему уравнений 
Итоговый самоконтроль
С-1. Как расположены комплексно-сопряженные числа в комплексной плоскости?
С-2. Определите модуль числа 
С-3. Чему равно значение  ?
?
С-4. Что собой представляет множество точек комплексной плоскости, для которых:
С-4.1. 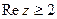 . С-4.2.
. С-4.2.  . С-4.3.
. С-4.3.  .
.
С-4.4.  . С-4.5.
. С-4.5.  ?
?
С-5. Где расположены действительные числа, мнимые числа в комплексной плоскости?
С-6. Следующие комплексные числа изобразить векторами и записать в тригонометрической и показательной формах, отметить на рисунке модуль и аргумент.
С-6.1. 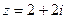 . С-6.2.
. С-6.2. 
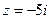 . С-6.3.
. С-6.3. 
С-7. Представить в алгебраической форме числа
С-7.1. 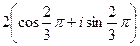 . С-7.2.
. С-7.2. 
С-8. Представить в тригонометрической форме комплексные числа:
С-8.1.  . С-8.2.
. С-8.2.  .
.
С-8.3. 
C-9. Найти наибольшее и наименьшее значения 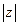 , если
, если 
С-10. При каких значениях  и
и  комплексные числа
комплексные числа  и
и 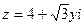 :
:
С-10.1. Равны? С-10.2. Сопряжены?
С-11. Могут ли быть сопряженными: два действительных числа? два чисто мнимых? действительное и мнимое число?
С-12. Пусть  Чему равен
Чему равен  ?
?
С-13. Какое из чисел больше:  или
или  ?
?
С-14. Найти действительные решения уравнения:
С-14.1.  . С-14.2.
. С-14.2. 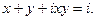
С-15. Вычислить 
С-16. Изобразить на комплексной плоскости множество точек  , удовлетворяющих условию
, удовлетворяющих условию
С-16.1. 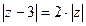 . С-16.2.
. С-16.2. 
С-17. Найти  и
и  , если:
, если:
С-17.1.  . С-17.2.
. С-17.2. 
С-18. Доказать справедливость тождества:
С-18.1.  . С-18.2.
. С-18.2. 
С-19. Дано  Найти
Найти  и
и 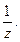
С-20. При каких действительных значениях  и
и  числа
числа  и
и  будут сопряженными?
будут сопряженными?
С-21. Может ли сумма квадратов двух комплексных чисел быть отрицательной?
4,3 КОМПЛЕКТЫ ЭКЗАМЕНАЦИОННЫХ БИЛЕТОВ ПО ЛИНЕЙНОЙ АЛГЕБРЕ
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Матрицы, линейные операции над матрицами, умножение матриц, транспонирование матриц. 2. Линейные пространства, подпространство линейного пространства. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 2 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Определители. Миноры и алгебраические дополнения элементов квадратной матрицы. 2. Евклидово пространство. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 3 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Критерий совместности системы линейных уравнений (теорема Кронекера-Капелли). 2. Переход к новому базису. Матрица перехода. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 4 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Системы линейных однородных уравнений. Критерий существования ненулевых решений у однородной системы. 2. Характеристический многочлен и его корни. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 5 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Линейная зависимость и независимость векторов. 2. Операции над множествами: объединение, пересечение, разность, прямое произведение двух множеств. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 6 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Метод Гаусса решения систем т уравнений с п неизвестными. 2. Арифметическое пространство Rn. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 7 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Скалярное произведение векторов, его свойства и механические приложения. 2. Закон инерции квадратичных форм. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Миноры матрицы. Определение ранга матрицы. Базисные миноры матрицы. 2. Критерий Сильвестра исследования знакоопределенности квадратичной формы. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 9 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Полярная система координат на плоскости. Связь с декартовой системой координат на плоскости. 2. Каноническое уравнение гиперболы, свойства кривой, эксцентриситет, полуоси, вершины, фокусы, директрисы и асимптоты. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 10 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Угол между двумя прямыми, заданными уравнениями с угловыми коэффициентами. Условия параллельности, перпендикулярности прямых на плоскости. 2. Положительно(отрицательно) полуопределенные квадратичные формы. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 11 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Базисные и свободные неизвестные. Нахождение общего и базисного решений системы линейных уравнений. 2. Отображения множеств. Взаимно-однозначное соответствие между множествами. Понятие числовой функции. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 12 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Алгоритм вычисления обратной матрицы (методом построения союзной матрицы). 2. Системы линейно зависимых и линейно независимых векторов. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 13 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Элементарные преобразования матрицы. Правило вычисления ранга матрицы с помощью элементарных преобразований. 2. Эквивалентные множества. Мощность множества. Счетные и несчетные множества. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 14 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Уравнение плоскости в трехмерном пространстве, проходящей через заданную точку перпендикулярно данному вектору. 2. Собственные векторы и собственные значения линейного оператора. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 15 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Прямая линия на плоскости: каноническое уравнение прямой, уравнение прямой, проходящей через 2 точки, параметрические уравнения прямой. 2. Линейные операторы. Матрица линейного оператора. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 16 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Системы линейных алгебраических уравнений: совместные и несовместные системы, определенные и неопределенные системы. 2. Ортонормированный базис. Процесс ортогонализации. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 17 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Решение систем линейных уравнений по формулам Крамера. 2. Размерность и базис линейного пространства. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 18 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Решение систем линейных уравнений матричным способом. 2. Алгоритм вычисления собственных векторов линейного оператора. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 19 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Свойства определителей. 2. Кривые второго порядка. Общее уравнение кривых 2-го порядка. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 20 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Построение фундаментальной системы решений для однородной системы линейных уравнений. 2. Линейная модель обмена. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 21 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Свободные векторы. Линейные операции над векторами. 2. Канонические уравнения параболы, свойства кривой, эксцентриситет, вершина, фокус, директриса. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 22 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Вычисление определителей второго и третьего порядков. 2. Уравнения некоторых трехмерных поверхностей (эллипсоид, однополостный гиперболоид, двуполостный гиперболоид, конус, эллиптический параболоид). 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 23 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Определение обратной матрицы. Теорема существования обратной матрицы. 2. Цилиндрические поверхности. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 24 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Правила вычисления определителей: разложение по элементам одной строки или столбца(теорема Лапласа), с помощью элементарных преобразований. 2. Квадратичные формы, матрица квадратичной формы. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 25 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Проекция вектора на ось. Координатное задание векторов. 2. Канонический вид квадратичной формы. Приведения квадратичной формы к каноническому виду. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 26 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Модель Леонтьева многоотраслевой экономики. 2. Понятие множества. Элемент множества, пустое множество. Круги Эйлера. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 27 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Векторное произведение векторов, его свойства и геометрические приложения. 2. Положительно(отрицательно) определенная квадратичная форма. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 28 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Смешанное произведение трех векторов, его свойства и геометрические приложения. 2. Равенство множеств. Подмножество. Универсальное множество. Дополнение множества. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №29 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Цилиндрическая и сферическая системы координат в пространстве. 2. Понятие математической структуры. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 30 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Аффинная система координат на плоскости и в пространстве. Прямоугольная декартова система координат на плоскости и в пространстве. 2. Основные законы операций над множествами. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 31 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Прямая линия на плоскости: уравнение прямой, проходящей через заданную точку перпендикулярно данному вектору, общее уравнение прямой, уравнение прямой в отрезках. 2. Множества точек на прямой и плоскости, задаваемые уравнениями и неравенствами. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 32 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Прямая линия на плоскости: уравнение прямой с угловым коэффициентом, уравнение пучка прямых, нормальное уравнение прямой; расстояние от точки до прямой. 2. Линейные пространства, подпространство линейного пространства. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 33 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Взаимное расположение прямых на плоскости. Угол между двумя прямыми, заданными общими уравнениями. Условия параллельности, перпендикулярности прямых на плоскости. 2. Евклидово пространство. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 34 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Общее уравнение плоскости. Частные случаи общего уравнения плоскости. 2. Основные алгебраические структуры: группы и полугруппы, кольца и поля. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 35 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Уравнение плоскости в отрезках. 2. Собственные векторы и собственные значения линейного оператора. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 36 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей. 2. Положительно(отрицательно) полуопределенные квадратичные формы. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 37 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Уравнения прямой в трехмерном пространстве: канонические, параметрические, общие уравнения прямой. 2. Матричные алгебраические структуры. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 38 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Угол между прямой и плоскостью в трехмерном пространстве. Условия параллельности и перпендикулярности прямой и плоскости. 2. Ортонормированный базис. Процесс ортогонализации. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 39 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Расстояние от точки до плоскости. 2. Множества точек на прямой и плоскости, задаваемые уравнениями и неравенствами. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 40 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Уравнения прямой в трехмерном пространстве, проходящей через две данные точки. 2. Матричные алгебраические структуры. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
| СОЧИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 41 дисциплина линейная алгебра курс 1 - ОФО специальности_______080101, 080102______________ 1. Угол между двумя прямыми в трехмерном пространстве, условия параллельности и перпендикулярности прямых. 2. Каноническое уравнение эллипса, свойства кривой, эксцентриситет, полуоси, вершины, фокусы, директрисы. 3. Задача. Утверждено на заседании кафедры Экзаменатор Якунина Н.Ф. “ 24 “ декабря 2011 г. Зав. кафедрой Макарова И.Л. |
Дата добавления: 2015-08-27; просмотров: 103 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение задач, связанных с различными уравнениями прямой и взаимным расположением прямых на плоскости | | | Распределение усыновлений иностранными гражданами по странам |