Свойства степенной функции с отрицательным рациональным показателем.
К началу страницы | К началу страницы | К началу страницы | К началу страницы | Свойства степенной функции с положительным рациональным показателем большим единицы. | Свойства степенной функции с отрицательным рациональным показателем. | Замечание. | Свойства степенной функции с отрицательным рациональным показателем. | Свойства степенной функции с отрицательным рациональным показателем. | Свойства степенной функции с отрицательным рациональным показателем. |
- Область определения:
 .
.
Поведение на границе области определения 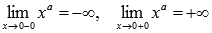 при
при  и а – несократимая рациональная дробь с нечетным и числителем и знаменателем.
и а – несократимая рациональная дробь с нечетным и числителем и знаменателем.
Следовательно, х = 0 является вертикальной асимптотой. - Область значений:
 .
. - Функция нечетная, так как
 .
. - Функция убывает при
 .
. - Функция выпуклая при
 и вогнутая при
и вогнутая при  .
. - Точек перегиба нет.
- Горизонтальной асимптотой является прямая y = 0.
- Функция проходит через точки (-1;-1), (1;1).
Разберемся со степенной функцией 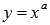 , когда
, когда  , числитель рациональной дроби в показателе степени представляет собой четное число, а знаменатель - нечетное число и сама дробь несократима (например, -6/5 или -24/7).
, числитель рациональной дроби в показателе степени представляет собой четное число, а знаменатель - нечетное число и сама дробь несократима (например, -6/5 или -24/7).
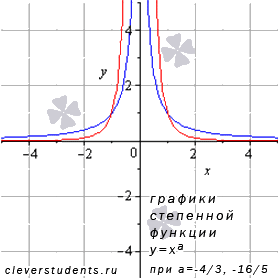
На иллюстрации взяты графики степенных функций  – синяя линия,
– синяя линия, 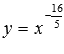 – красная линия.
– красная линия.
Дата добавления: 2015-08-27; просмотров: 47 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.012 сек.)

 .
.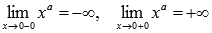 при
при  и а – несократимая рациональная дробь с нечетным и числителем и знаменателем.
и а – несократимая рациональная дробь с нечетным и числителем и знаменателем. .
.  .
.  .
.  и вогнутая при
и вогнутая при  .
. 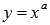 , когда
, когда  , числитель рациональной дроби в показателе степени представляет собой четное число, а знаменатель - нечетное число и сама дробь несократима (например, -6/5 или -24/7).
, числитель рациональной дроби в показателе степени представляет собой четное число, а знаменатель - нечетное число и сама дробь несократима (например, -6/5 или -24/7).
 – синяя линия,
– синяя линия, 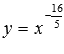 – красная линия.
– красная линия.