Свойства числовых последовательностей

Числовая последовательность — частный случай числовой функции, а потому некоторые свойства функций (ограниченность, монотонность) рассматривают и для последовательностей.

Определение 2. Последовательность (у„) называют ограниченной сверху, если все ее члены не больше некоторого числа.

Иными словами, последовательность (у„) ограничена сверху, если существует числом такое, что для любого л выполняется неравенство у_n<М. Число М называют верхней границей последовательности.

Например, последовательность -1, -4, -9, -16,...,-п2,... ограничена сверху. В качестве верхней границы можно взятьчисло -1 или любое число, которое больше, чем -1, например 0.

Определение 3. Последовательность (у„) называют ограниченной снизу, если все ее члены не меньше некоторого числа.

Иными словами, последовательность (у_n) ограничена снизу, если существует число т такое, что для любого л выполняется неравенство у„>M. Число m называют нижней границей последовательности.

Например, последовательность 1, 4, 9, 16,..., п2,... ограничена снизу. В качестве нижней границы можно взять число 1 или любое число меньше 1.

Если последовательность ограничена и сверху, и снизу, то ее называют ограниченной. Например, Эта последовательность ограничена и сверху, и снизу. В качестве верхней границы можно взять число 1, в качестве нижней границы — число 0.

Если построить график последовательности

в прямоугольной системе координат, то окажется, что весь он расположен в полосе между некоторыми горизонтальными прямыми, например, у=0, и у = 1 (рис. 97), а в зтом и состоит, как известно, геометрический признак ограниченности функции.

Особенно наглядным становится свойство ограниченности последовательности, если члены последовательности отметить точками на числовой прямой. Ограниченность последовательности означает, что все члены последовательности (точнее, соответствующие им точки прямой) принадлежат некоторому отрезку. Так, изобразив члены последовательности точками на числовой прямой, замечаем, что все они принадлежат отрезку [0, 1] (рис. 98).

Определение 4. Последовательность (у„) называют возрастающей, если каждый ее член больше предыдущего:

Например, 1, 3, 5, 7.....2n -1,... — возрастающая последовательность.

Определение 5. Последовательность (у„) называют убывающей, если каждый ее член меньше предыдущего:

Например, убывающая последовательность.
Возрастающие и убывающие последовательности объединяют общим термином — монотонные последовательности. Приведем еще несколько примеров.
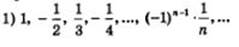Эта последовательность не является ни возрастающей, ни убывающей (немонотбнная последовательность).
2) у_n =2ⁿ. Речь идет о последовательности 2, 4, 8, 16, 32,... Это — возрастающая последовательность.
Вообще, если а > 1, то последовательность у_n =аⁿ возрастает.

Речь идет о последовательности
Это — убывающая последовательность.
Вообще, если 0 <а < 1, то последовательность у_n =аⁿ убывает

Дата добавления: 2015-08-27