Числовые последовательности

1. Определение числовой последовательности и способы ее задания.

Что такое числовая последовательность и как она задается, вам известно из курса алгебры 9-го класса. Напомним соответствующее определение.

Определение 1. Функцию вида 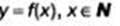называют функцией натурального аргумента или числовой последовательностью и обозначают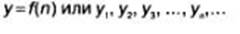

Иногда для обозначения последовательности используется запись (у_n).

Последовательности можно задавать различными способами, например словесно, когда правило задания последовательности описано словами, без указания каких-то формул. Так, словесно задается последовательность простых чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29,...

Особенно важны аналитический и рекуррентный способы задания последовательности.

Говорят, что последовательность задана аналитически, если указана формула ее п-го члена.

Приведем три примера.

1) у_п =п². Это — аналитическое задание последовательности
1,4, 9,16,...,п²,...

Указав конкретное значение п, нетрудно найти член последовательности с соответствующим номером. Если, например, п =9, 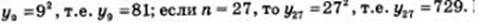Напротив, если взят определенный член последовательности, можно указать его номер. Например, если у_п =625, то из уравнения п² =625 находим, что п =25. Это значит, что 25-й член заданной последовательности равен 625.

2) у_п =С. Здесь речь идет о последовательности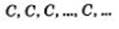

Такую последовательность называют постоянной (или стационарной).

3) у_п =2ⁿ. Это — аналитическое задание последовательности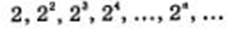

Рекуррентный способ задания последовательности состоит в том, что указывают правило, позволяющее вычислить п-й член последовательности, если известны ее предыдущие члены. Например, арифметическая прогрессия — это числовая последовательность (а„), заданная рекуррентно соотношениями:

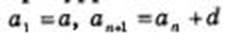
Геометрическая прогрессия — это числовая последовательность, заданная рекуррентно соотношениями:

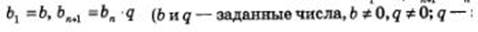— знаменатель геометрической прогрессии). Прогрессии вы изучали в курсе алгебры 9-го класса.

Дата добавления: 2015-08-27