Предел функции нескольких переменных

Функция f (M) = f (x ₁, x ₂, …, x_n) имеет предел А R^m при стремлении переменных M (x ₁, x ₂, …, x_n) R ⁿ к величинам M₀(a ₁, a ₂, …, a_n) Rⁿ, если для любого как угодно малого положительного числа ε > 0 существует положительное и зависящее от этого ε число δ, что для всех точек М (x ₁, x ₂, …, x_n) Rⁿ попадающих в δ окрестность точки М₀ значения функции попадают в ε окрестность точки А:

( ε > 0) ( δ = δ(ε) > 0) ( M O_δ (M ₀ ) \ {M₀}): f (M) O_ε(A).

Точка М может и не совпадать с М₀. Следует отметить, что этот предел должен существовать и не зависеть от способа стремления переменных (x ₁, x ₂, …, x_n) к величинам (a ₁, a ₂, …, a_n).
Это свойство можно записать так

.

На основании леммы п. 1 можно утверждать, что стремление к точке означает координатную сходимость

.

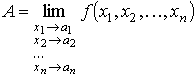
Независимость стремления переменной точки к точке сгущения означает, что

.

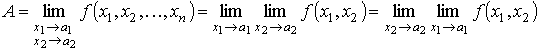Рассмотрим примеры, которые иллюстрируют зависимость значения предела от характера стремления текущей точки к точке сгущения, что означает отсутствие предела.
Пример 1. Рассмотрим предел функции

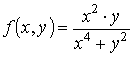
при стремлении к началу координат по прямым у = k·x:

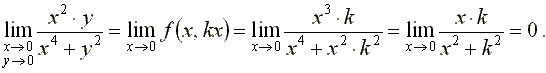
Рассмотрим предел той же функции при стремлении к началу координат по параболам у = а·х ²:

,

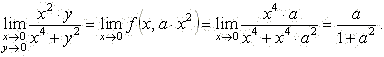и получается, что каждой параболе соответствует своё значение предела. Что свидетельствует о зависимости предела от способа стремления текущей точки к точке сгущения. Это означает, что данная функция не имеет предела в начале координат.
Пример 2. Рассмотрим предел функции

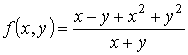, (х, у) ≠ (0, 0)

при стремлении текущей точки к началу координат. Непосредственно имеем

,
.

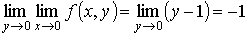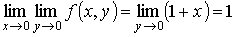Видно, что значение предела зависит от способа стремления текущей точки к началу координат

.

Теорема 1. Если

• 1) существует двойной предел

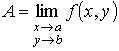(1.1)

• 2) при любом y существует простой предел по переменной х:

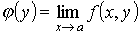
то существует повторный предел

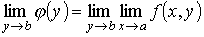
и он равен значению двойного предела А.

Доказательство. Соотношение (1.1) означает, что

( ε > 0) ( δ = δ (ε, M₀) > 0) ( 0 < | x – a | < δ, 0 < | y - b | < δ)): | f (x, y) – A| < ε

Зафиксируем переменную у в интервале 0 < | у - b | < δ и перейдём к пределу в неравенстве | f (x, y) - А | < δ при х → а. Получим | φ(y) - А| < ε, где 0 < | у - b | < δ, что означает

.

Дата добавления: 2015-08-27