|
Читайте также: |
Для чего нужно классифицировать элементарные функции?
Ответ очень прост: каждому классу функций соответствует определенный набор свойств. Некоторые функции бесконечное число раз дифференцируемы на каком-либо промежутке, некоторые непрерывны, другие ортогональны с весом и т.д. и т.п.
Согласитесь, когда все книги разложены по-полочкам по определенным тематикам, достаточно просто найти нужную...
Определение элементарной функции.
Функции, которые могут быть получены из основных элементарных функций посредством арифметических действий (сложение, вычитание, умножение, деление) и образования сложных функций, называются элементарными функциями.
Примером может являться функция 
Очень удобно классификацию элементарных функций представить в виде таблицы.
Элементарные функции подразделяются на алгебраические и трансцендентные.
Определение алгебраических функций.
Алгебраическими называют функции, составленные из букв и цифр, соединенных знаками действий сложение, умножение, вычитание, деление, возведение в целую степень и извлечение корня.
Другими словами: алгебраическими называют элементарные функции, которые могут быть получены из двух основных функций f(x)=x и f(x)=1 при помощи любого числа последовательно выполненных алгебраических действий (сложение, умножение, вычитание, деление, возведение в целую степень, извлечение корня) и умножения на числовые коэффициенты.
Например, функция 
является алгебраической.
Определение трансцендентной функции.
Трансцендентными называют элементарные функции, которые не являются алгебраическими. (То есть, они образованы при помощи возведения в иррациональную степень, логарифмирования, с использованием тригонометрических и обратных тригонометрических операций).
К примеру, 
- трансцендентная функция.
Алгебраические функции подразделяются на рациональные и иррациональные.
Рациональные функции разделяются на целые рациональные функции (многочлены) и дробные рациональные (отношение многочленов).
Пример целой рациональной функции: 
.
Пример дробно-рациональной функции: 
.
ПРИМЕЧАНИЕ:
Рациональные функции могут содержать и иррациональные коэффициенты (главное, чтобы под знаком радикала не было аргумента функции). Например,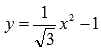 
- целая рациональная функция, а не иррациональная.
Определение иррациональной функции.
Иррациональными называются алгебраические функции, содержащие аргумент под знаком радикала (корня).
Примером может являться функция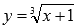 
.
ПРИМЕЧАНИЕ:
Если вид функции можно упростить на всей области определения, то классификации подлежит именно упрощенная функция.
Дата добавления: 2015-08-27; просмотров: 118 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства непрерывных функций | | | Множество значений функции. |