Множество значений функции.

Дадим краткое описание тех понятий, которые включены нами в схему исследования функции.

Область определения – множество значений аргумента, при которых задана функция. Если функция задана формулой, то имеется в виду ее естественная область определения, т. е. множество чисел, к которым применима данная формула.

Примеры

а) y = x ² – 1, D: R, или x – любое число.

б) 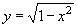, D: [–1; 1].

в) 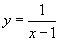, D: x ¹ 1, или x – любое число, кроме x = 1.

г) 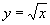, D: [0; +¥), или x – любое неотрицательное число.

Во всех этих примерах указывалась естественная область определения функции.

Нули (корни) – точки, в которых функция обращается в нуль, или, иначе, решения уравнения f (x) = 0.

Примеры

а) y = 2 x – 1, один нуль: .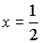

б) y = x ² + x – 2, нули: x ₁ = 1, x ₂ = –2.

в) y = x ² + x + 2, нулей нет.

г) y = x – [ x ], нули: все целые числа.

Промежутки знакопостоянства – интервалы, на которых функция положительна или отрицательна, или, иначе, решения неравенств f (x) > 0 и f (x) < 0.

Примеры

а) 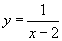, y < 0 при x < 2; y > 0 при x > 2, или y < 0 при
x Î (–¥; 2), y > 0 при x Î (2; +¥).

б) , y < 0 при x Î (0; 4), y > 0 при x Î (4; +¥).

в) 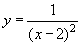, y > 0 при всех допустимых значениях x, или при x Î (–¥; 2) È (2; +¥).

г) 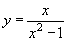, y < 0 при x Î (–¥; –1) È (0; 1); y > 0 при x Î (–1; 0) È (1; +¥).

Точки экстремума – точки, лежащие внутри области определения, в которых функция принимает самое большое (максимум) или самое малое (минимум) значение по сравнению со значениями в близких точках.

Примеры

а) 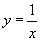, экстремумов нет.

б) y = x ² – 2 x, x = 1 – точка минимума. Значение в этой точке равно –1: y (1) = –1.

в) ,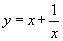

x = –1 – точка максимума, y (–1) = –2;
x = +1 – точка минимума, y (+1) = 2.

г) y = | x |, x = 0 – точка минимума, y (0) = 0.

Промежутки возрастания и убывания – интервалы, на которых функция или возрастает, или убывает. Слова “возрастание” и “убывание” функции иногда заменяют одним словом – “монотонность” функции.

Примеры

а) y = 1 – x, y убывает на всей числовой оси.

б) y = x ² – 1, y убывает на промежутке (–¥; 0] и возрастает на промежутке [0; +¥).

в) 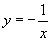, y возрастает на каждом из промежутков (–¥; 0) и (0; +¥).

г) y = x ³ + x, y возрастает на всей числовой оси.

Наибольшее и наименьшее значения функции – самое большое или самое маленькое значение функции по сравнению со всеми возможными (в отличие от экстремумов, где сравнение ведется только с близкими точками).

Примеры

а) y = 1 – x; функция не имеет ни наибольшего, ни наименьшего значений.

б) y = – x, x Î [–1; 1]; наибольшее и наименьшее значения функция принимает на концах промежутка: y (–1) = 1 – наибольшее значение; y (1) = 1 – наименьшее значение.

в) y = x ² – 1; наименьшее значение функция принимает при x = 0,

y (0) = –1. Наибольшего значения у функции нет.

г) y = – x ² + 2 x, x Î [1; 3], наибольшее и наименьшее значения функция принимает на концах промежутка: y (1) = 1 – наибольшее значение;

y (3) = –3 – наименьшее значение.

Множество значений функции – множество чисел, состоящее из всех значений функции.

Примеры

а) y = – x, Е: R, или y – любое число.

б) y = – x, x Î [–1; 1]. Е: [–1; 1].

в) y = x ² – 1, E: [–1; +¥).

г) y = – x ² + 2 x, x Î [0; 3], Е: [–3; 1], или –3 £ y £ 1.

Дата добавления: 2015-08-27