Теорема 4 (свойства бесконечно малых функций).

1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

2. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая.

3. Произведение конечного числа бесконечно малых является бесконечно малой.

Доказательство. Докажем для примера первое утверждение теоремы для двух бесконечно малых.

Из того, что существует lim_{x® a}a(x) = 0, следует, что " e>0 $ d₁(e)>0 такое, что " x: 0<|x-a|<d₁ выполняется неравенство
|a(x)|< e/2. Аналогично, из существования предела lim_{x® a} b(x) = 0, следует " e>0 $ d₂(e)>0 такое, что " x: 0<|x-a|<d₂
выполняется неравенство |b(x)|< e/2. Тогда " x: 0<|x-a|<d = min{d₁,d₂} выполнятся оба неравенства одновременно, то есть

| a(x)+b(x) | £ | a(x) |+| b(x) |< e.

32) Связь бесконечно малых и бесконечно больших величин.

Вторым важным случаем при вычислении предела функции является понятие бесконечно большой величины.

Определение. Функция называется бесконечно большой величиной при , если .

Основываясь на определении предела функции, охарактеризуем бесконечно большую величину иначе. Если , то

.

Значит, бесконечно большая величина это функция, которая может стать больше любого наперед заданного положительного числа.

Аналогичное определение вводится и для случаев, когда .

Между бесконечно большими и бесконечно малыми величинами существует тесная связь, которая устанавливается следующими теоремами.

Теорема 9.1.1. Если функция является бесконечно большой величиной при , то – бесконечно малая величина при .

Доказательство. Возьмем произвольное число . Так как – бесконечно большая величина при , то, согласно определению, как только , получим . Но тогда , то есть является бесконечно малой величиной, что и требовалось доказать.

Теорема 9.1.2. Если функция является бесконечно малой величиной при , то – бесконечно большая величина при .

Доказательство. Возьмем произвольное число . Так как – бесконечно малая величина при , то, согласно определению, как только , получаем . Но тогда , то есть является бесконечно большой величиной, что и требовалось доказать.

Так как бесконечно большие и бесконечно малые величины связаны между собой, то свойства бесконечно большой величины такие же, как и у бесконечно малой.

33) Свойства пределов.

Обозначение предела Предел функции обозначается как , при или через символ предела .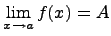

Дата добавления: 2015-08-27